
【题目】已知椭圆![]() 上一点
上一点![]() 与椭圆右焦点的连线垂直于x轴,直线l:y=kx+m与椭圆C相交于A,B两点(均不在坐标轴上).
与椭圆右焦点的连线垂直于x轴,直线l:y=kx+m与椭圆C相交于A,B两点(均不在坐标轴上).
(1)求椭圆C的标准方程;
(2)设O为坐标原点,若△AOB的面积为![]() ,试判断直线OA与OB的斜率之积是否为定值?若是请求出,若不是请说明理由.
,试判断直线OA与OB的斜率之积是否为定值?若是请求出,若不是请说明理由.
【答案】(1)![]() ;(2)定值
;(2)定值![]()
【解析】
(1)根据条件,代入已知点,和a,b,c的关系式,解得参数值,进而得到椭圆方程;(2)联立直线和椭圆方程得到二次方程,由三角形的面积得到4k2+3-2m2=0,kOA·kOB=![]() ,根据韦达定理得到结果即可.
,根据韦达定理得到结果即可.
(1)由题意知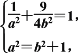 解得
解得![]()
∴椭圆C的标准方程为![]() +
+![]() =1.
=1.
(2)设点A(x1,y1),B(x2,y2),
由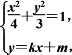 得(4k2+3)x2+8kmx+4m2-12=0,
得(4k2+3)x2+8kmx+4m2-12=0,
由Δ=(8km)2-16(4k2+3)(m2-3)>0,得m2<4k2+3.
∵x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴S△OAB=![]() |m||x1-x2|=
|m||x1-x2|=![]() |m|·
|m|·![]() =
=![]() ,
,
化简得4k2+3-2m2=0,满足Δ>0,从而有4k2-m2=m2-3(*),
∴kOA·kOB=![]() =
=![]() =
=
=![]() ,由(*)式,得
,由(*)式,得![]() =1,
=1,
∴kOA·kOB=-![]() ,即直线OA与OB的斜率之积为定值-
,即直线OA与OB的斜率之积为定值-![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N* , 存在实数x使f(x)<2成立.
(Ⅰ)求实数m的值;
(Ⅱ)若α,β>1,f(α)+f(β)=2,求证: ![]() +
+ ![]() ≥
≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n为不重合的两条直线,![]() ,
,![]() 为不重合的两个平面,则下列命题中,所有真命题的个数是______.
为不重合的两个平面,则下列命题中,所有真命题的个数是______.
![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;
![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;![]() 一定存在直线l,使得
一定存在直线l,使得![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ax2+x﹣1)ex , 其中e是自然对数的底数,a∈R.
(Ⅰ)若a=1.求曲线f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若a=﹣1,函数f(x)的图象与函数g(x)=![]() x3+
x3+![]() x2+m的图象有3个不同的交点,求实数m的取值范围.
x2+m的图象有3个不同的交点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 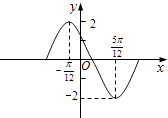
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京故宫博物院成立于1925年10月10日,是在明、清朝两代皇宫及其宫廷收藏的基础上建立起来的中国综合性博物馆,每年吸引着大批游客参观游览![]() 下图是从2012年到2017年每年参观人数的折线图
下图是从2012年到2017年每年参观人数的折线图![]() 根据图中信息,下列结论中正确的是
根据图中信息,下列结论中正确的是![]()
![]()
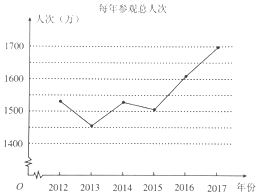
A. 2013年以来,每年参观总人次逐年递增
B. 2014年比2013年增加的参观人次不超过50万
C. 2012年到2017年这六年间,2017年参观总人次最多
D. 2012年到2017年这六年间,平均每年参观总人次超过160万
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C以坐标轴为对称轴,以坐标原点为对称中心,椭圆的一个焦点为![]() ,点
,点![]() 在椭圆上,
在椭圆上,
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程.
求椭圆C的方程.
![]() Ⅱ
Ⅱ![]() 斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为正数,给出下列命题:
①若a2﹣b2=1,则a﹣b<1;
②若 ![]() ﹣
﹣ ![]() =1,则a﹣b<1;
=1,则a﹣b<1;
③ea﹣eb=1,则a﹣b<1;
④若lna﹣lnb=1,则a﹣b<1.
期中真命题的有
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com