Question

过曲线C：y=x³上的点P₁（x₁，y₁）作曲线C的切线l₁与曲线C交于点P₂（x₂，y₂），过点P₂作曲线C的切线l₂与曲线C交于点，依此类推，可得到点列：P₁（x₁，y₁），P₂（x₂，y₂），P₃（x₃，y₃），…，P_n（x_n，y_n），…，已知x₁=1．
（1）求点P₂、P₃的坐标；
（2）求数列{x_n}的通项公式；
（3）记点P_n到直线l_n+1（即直线P_n+1P_n+2）的距离为d_n，求证：

1

d1

+

1

d 2

+…+

1

dn

＞

4

9

．

Answer 1

分析：（1）由题意因为x₁=1，且已知过曲线C：y=x³上的点P₁（x₁，y₁），把点的坐标代入得P₁（1，1），再由题意可以得到P₂，P₃；
（2）由题意及导数的几何含义及题中P₁（x₁，y₁），P₂（x₂，y₂），P₃（x₃，y₃），…，P_n（x_n，y_n），…，的产生可以得到数列{x_n}的通项公式；
（3）有（2）知道点P_n的坐标，利用电到直线的距离公式得到点P_n到直线l_n+1（即直线P_n+1P_n+2）的距离为d_n，在有得到式子放缩一下即可．

解答：解：（1）因为x₁=1，且已知过曲线C：y=x³上的点P₁（x₁，y₁），所以得P₁（1，1），再由题意可以得P₂（-2，-8），P₃（4，64）．
（2）曲线C上点P_n（x_n，y_n）处的切线l_n的斜率为kn=y′x=xn=3

x

2 n

，
故得到切线的方程为y-y_n=3x_n²•（x-x_n），
联立方程

y=x3 y-yn=3 x 2 n •(x-xn) yn= x 3 n

消去y，y_n得：x³-3x_n²•x+2x_n³=0
化简得：（x-x_n）²•（x+2x_n）=0所以：x=x_n或x=-2x_n，
由x=x_n得到点P_n的坐标（x_n，y_n），由x=-2x_n就得到点P_n+1的坐标（-2x_n，（-2x_n）³）所以：x_n+1=-2x_n故数列{x_n}为首项为1，公比为-2的等比数列所以：x_n=（-2）^n-1
（3）由（2）知：P_n+1（（-2）ⁿ，（-8）ⁿ），P_n+2（（-2）ⁿ⁺¹，（-8）ⁿ⁺¹），
所以直线l_n的方程为：y-(-8)n=

(-8)n-(-8)n+1

(-2)n-(-2)n+1

(x-(-2)n)
化简得：3•4ⁿx-y-2•（-8）ⁿ=0，dn=

|3•4n•(-2)n-1-(-8)n-1-2•(-8)n|

(3•4n)2+(-1)2

=

27•8n-1

9•42n+1

＜

27•8n-1

3•22n

=9•2n-3
所以

1

dn

＞

1

9

•(

1

2

)n-3
∴

1

d1

+

1

d2

++

1

dn

＞

8

9

(1-

1

2n

)≥

8

9

(1-

1

2

)=

4

9

点评：此题考查了学生对于题意的准确理解，还考查了利用导数的几何意义求曲线上一点的切线的斜率及利用点斜式求出直线的方程，还考查了一元三次方程的求解及证明不等式时的恰当放缩．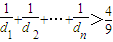