
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,且椭圆四个顶点构成的菱形面积为
,且椭圆四个顶点构成的菱形面积为![]() .
.
(1)求椭圆C的方程;
(2)若直线l :y=x+m与椭圆C交于M,N两点,以MN为底边作等腰三角形,顶点为P(3,-2),求m的值及△PMN的面积.
科目:高中数学 来源: 题型:
【题目】已知直线l方程为(m+2)x-(m+1)y-3m-7=0,m∈R.
(Ⅰ)求证:直线l恒过定点P,并求出定点P的坐标;
(Ⅱ)若直线l在x轴,y轴上的截距相等,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:A,1.5小时以上,B,1-1.5小时,C,0.5-1小时,D,0.5小时以下.图(1),(2)是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
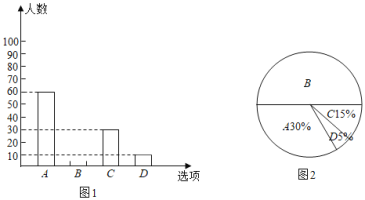
(1)本次一共调查了多少名学生.
(2)在图(1)中将![]() 对应的部分补充完整.
对应的部分补充完整.
(3)若该校有3000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)如图(1)所示,椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,求此椭圆的离心率;
(2)如图(2)所示,双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,求此双曲线的离心率.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质检部门对某工厂甲、乙两个车间生产的![]() 个零件质量进行检测.甲、乙两个车间的零件质量(单位:克)分布的茎叶图如图所示.零件质量不超过
个零件质量进行检测.甲、乙两个车间的零件质量(单位:克)分布的茎叶图如图所示.零件质量不超过![]() 克的为合格.
克的为合格.
(1)质检部门从甲车间![]() 个零件中随机抽取
个零件中随机抽取![]() 件进行检测,若至少
件进行检测,若至少![]() 件合格,检测即可通过,若至少
件合格,检测即可通过,若至少![]() 件合格,检测即为良好,求甲车间在这次检测通过的条件下,获得检测良好的概率;
件合格,检测即为良好,求甲车间在这次检测通过的条件下,获得检测良好的概率;
(2)若从甲、乙两车间![]() 个零件中随机抽取
个零件中随机抽取![]() 个零件,用
个零件,用![]() 表示乙车间的零件个数,求
表示乙车间的零件个数,求![]() 的分布列与数学期望.
的分布列与数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() .
.
(1)若直线![]() 过点
过点![]() 且到圆心
且到圆心![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 的斜率为负),当
的斜率为负),当![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com