
(1)求f(1)及f(![]() )的值(写成关于p的表达式);
)的值(写成关于p的表达式);
(2)求证:f(x)在(0,+∞)上是减函数;
(3)设an=f(2n),n∈N,求数列{an}的通项公式an(关于p的表达式).
(1)解:取a=b=1,则f(1)=2f(1)-p,故f(1)=p.
又f(1)=f(2·![]() )=f(2)+f(
)=f(2)+f(![]() )-p,且f(2)=p-1,得f(
)-p,且f(2)=p-1,得f(![]() )=f(1)-f(2)+p=p-(p-1)+p=p+1.
)=f(1)-f(2)+p=p-(p-1)+p=p+1.
(2)证明:设0<x1<x2,
∴f(x2)-f(x1)=f(![]() ·x1)-f(x1)
·x1)-f(x1)
=[f(![]() )+f(x1)-p]-f(x1)
)+f(x1)-p]-f(x1)
=f(![]() )-p.
)-p.
依0<x1<x2,可得![]() >1.
>1.
又依据当x>1时,总有f(x)<p成立,可得f(![]() )<p.
)<p.
∴f(x2)-f(x1)<0.故f(x)在(0,+∞)上是减函数.
(3)解:∵an=f(2n),
∴a n+1=f(2n+1)=f(2·2n)=f(2)+f(2n)-p=(p-1)+an-p=an-1.
∴a n+1-an=-1.
又a1=f(2)=p-1,∴数列{an}是以a1=p-1为首项,公差为-1的等差数列.
∴an=a1+(n-1)d=(p-1)-(n-1)=-n+p.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
| 1 |
| 3n |
| 2 |
| 3n |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练2练习卷(解析版) 题型:解答题
设定义在(0,+∞)上的函数f(x)=ax+ +b(a>0).
+b(a>0).
(1)求f(x)的最小值;
(2)若曲线y=f(x)在点(1,f(1))处的切线方程为y= x,求a,b的值.
x,求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省云浮市高三第五次月考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)设定义在(0,+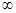 )上的函数
)上的函数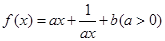
(Ⅰ)求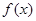 的最小值;
的最小值;
(II)若曲线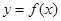 在点
在点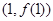 处的切线方程为
处的切线方程为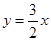 ,求
,求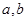 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com