
【题目】在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,过
,过![]() 三点的的平面截去长方体的一个角后.得到如图所示的几何体
三点的的平面截去长方体的一个角后.得到如图所示的几何体![]() ,且这个几何体的体积为
,且这个几何体的体积为![]() .
.
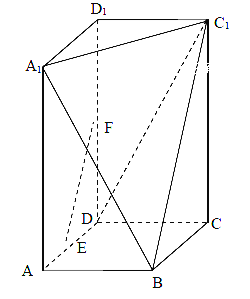
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 的长;
的长;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与
与![]() 垂直,如果存在,求线段
垂直,如果存在,求线段![]() 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
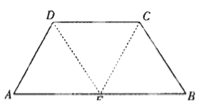
【题目】【2017开封高三模拟理】如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点.将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了了解全校学生的阅读情况,在全校采用随机抽样的方法抽取了60名学生(其中初中组和高中组各30名)进行问卷调查,并将他们在一个月内去图书馆的次数进行了统计,将每组学生去图书馆的次数分为5组: ![]() ,分别制作了如图所示的频率分布表和频率分布直方图.
,分别制作了如图所示的频率分布表和频率分布直方图.
分组 | 人数 | 频率 |
| 3 | |
| 9 | |
| 9 | |
| 0.2 | |
| 0.1 |
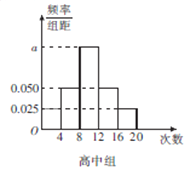
(1)完成频率分布表,并求出频率分布直方图中![]() 的值;
的值;
(2)在抽取的60名学生中,从在一个月内去图书馆的次数不少于16次的学生中随机抽取3人,并用![]() 表示抽得的高中组的人数,求
表示抽得的高中组的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宋元时期杰出的数学家朱世杰在其数学巨著《四元玉鉴》卷中“茭草形段”第一个问题“今有茭草六百八十束,欲令‘落一形’埵(同垛)之.问底子(每层三角形边茭草束数,等价于层数)几何?”中探讨了“垛枳术”中的落一形垛(“落一形”即是指顶上1束,下一层3束,再下一层6束,…,成三角锥的堆垛,故也称三角垛,如图,表示第二层开始的每层茭草束数),则本问题中三角垛底层茭草总束数为 .

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
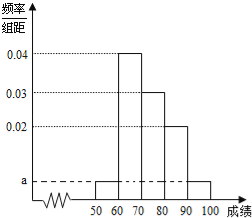
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[50,90)之外的人数.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月13日第30届大连国际马拉松赛举行,某单位的10名跑友报名参加了半程马拉松、10公里健身跑、迷你马拉松3个项目(每人只报一项),报名情况如下:
项目 | 半程马拉松 | 10公里健身跑 | 迷你马拉松 |
人数 | 2 | 3 | 5 |
(其中:半程马拉松![]() 公里,迷你马拉松
公里,迷你马拉松![]() 公里)
公里)
(1)从10人中选出2人,求选出的两人赛程距离之差大于10公里的概率;
(2)从10人中选出2人,设![]() 为选出的两人赛程距离之和,求随机变量
为选出的两人赛程距离之和,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com