
【题目】已知圆![]() ,圆
,圆![]() 过
过![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() (
(![]() 在第二象限).
在第二象限).
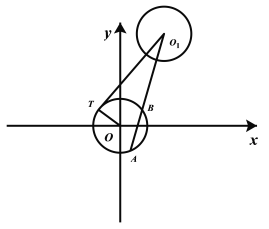
(1)求![]() 的正弦值;
的正弦值;
(2)已知点![]() ,过
,过![]() 点分别作两圆切线,若切线长相等,求
点分别作两圆切线,若切线长相等,求![]() 关系;
关系;
(3)是否存在定点![]() ,使过点
,使过点![]() 有无数对相互垂直的直线
有无数对相互垂直的直线![]() 满足
满足![]() ,且它们分别被圆
,且它们分别被圆![]() 、圆
、圆![]() 所截得的弦长相等?若存在,求出所有的点
所截得的弦长相等?若存在,求出所有的点![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 存在且其坐标为
存在且其坐标为![]() 或者
或者![]() .
.
【解析】
(1)连接![]() ,利用
,利用![]() 可求
可求![]() 的正弦值.
的正弦值.
(2)利用直线与圆相切求出过![]() 且与两圆相切的切线长,整理后可得所求的
且与两圆相切的切线长,整理后可得所求的![]() 关系式.
关系式.
(3)设![]() 的斜率为
的斜率为![]() 且
且![]() ,利用
,利用![]() 、
、![]() 分别被圆
分别被圆![]() 、圆
、圆![]() 所截得的弦长相等且两圆半径相等得到
所截得的弦长相等且两圆半径相等得到![]() 对无穷多个
对无穷多个![]() 恒成立,整理后可得关于
恒成立,整理后可得关于![]() 的方程组,从而可求
的方程组,从而可求![]() 的坐标.
的坐标.
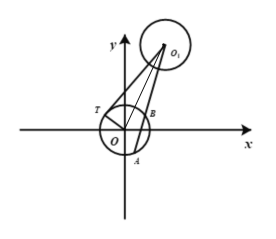
(1)连接![]() ,因为
,因为![]() 与
与![]() 相切于
相切于![]() ,故
,故![]() .
.
又![]() ,
,
在![]() 中,
中,![]() ,故
,故![]() .
.
(2)因为过![]() 作两圆的切线且切线长相等,
作两圆的切线且切线长相等,
故![]() ,整理得到
,整理得到![]() ,
,
故![]() 的关系为
的关系为![]() .
.
(3)设![]() 的斜率为
的斜率为![]() 且
且![]() ,
,
则![]() ,
,![]() ,
,
因为它们分别被圆![]() 、圆
、圆![]() 所截得的弦长相等且两圆半径相等,
所截得的弦长相等且两圆半径相等,
所以![]() 到直线
到直线![]() 的距离等于
的距离等于![]() 到直线
到直线![]() 的距离,
的距离,
故![]() 即
即![]() 对无穷多个
对无穷多个![]() 恒成立,
恒成立,
所以![]() 对无穷多个
对无穷多个![]() 恒成立.
恒成立.
故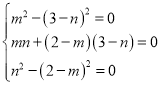 ,解得
,解得 或者
或者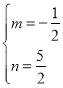 .
.
故![]() 存在且其坐标为
存在且其坐标为![]() 或者
或者![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减,②存在常数
上单调递减,②存在常数![]() ,使其值域为
,使其值域为![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的“渐近函数”.
的“渐近函数”.
(1)判断函数![]() 是不是函数
是不是函数![]() 的“渐近函数”,说明理由;
的“渐近函数”,说明理由;
(2)求证:函数![]() 不是函数
不是函数![]() 的“渐近函数”;
的“渐近函数”;
(3)若函数![]() ,
,![]() ,求证:当且仅当
,求证:当且仅当![]() 时,
时,![]() 是
是![]() 的“渐近函数”.
的“渐近函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
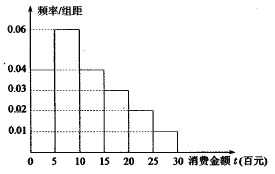
【题目】“双十一”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额![]() (百元)的频率分布直方图如图所示:
(百元)的频率分布直方图如图所示:
(1)求网民消费金额![]() 的平均值和中位数
的平均值和中位数![]() ;
;
(2)把下表中空格里的数填上,能否有![]() 的把握认为网购消费与性别有关;
的把握认为网购消费与性别有关;
男 | 女 | 合计 | |
| |||
| 30 | ||
合计 | 45 |
附表:
|
|
|
|
|
|
|
|
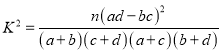 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是


A. A B. B C. C D. D
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为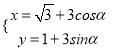 (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为非负半轴为极轴建立极坐标系.
轴为非负半轴为极轴建立极坐标系.
(1)求圆![]() 的普通方程与极坐标方程;
的普通方程与极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,求圆
,求圆![]() 上的点到直线
上的点到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 的三等分点(如图1).将
的三等分点(如图1).将![]() 沿着
沿着![]() 折起到
折起到![]() 的位置,连接
的位置,连接![]() (如图2).
(如图2).

(1)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(2)记线段![]() 的中点为
的中点为![]() ,平面
,平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有6个完全相同的小球,分别标号为1,2,3,4,5,6.
(1)一次取出两个小球,求其号码之和能被3整除的概率;
(2)有放回的取球两次,每次取一个,求两个小球号码是相邻整数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间中,下列命题正确的是
A.如果一个角的两边和另一角的两边分别平行,那么这两个角相等
B.两条异面直线所成的有的范围是![]()
C.如果两个平行平面同时与第三个平面相交,那么它们的交线平行
D.如果一条直线和平面内的一条直线平行,那么这条直线和这个平面平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com