
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过椭圆C的右焦点且垂直于x轴的直线与椭圆交于A,B两点,且|AB|=
,过椭圆C的右焦点且垂直于x轴的直线与椭圆交于A,B两点,且|AB|= ![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点(1,0)的直线l交椭圆C于E,F两点,若存在点G(﹣1,y0)使△EFG为等边三角形,求直线l的方程.
【答案】解:(Ⅰ)由椭圆的离心率e= ![]() =
= ![]() ,①由椭圆的通径丨AB丨=
,①由椭圆的通径丨AB丨= ![]() =
= ![]() ,② 由a2=b2+c2 , ③
,② 由a2=b2+c2 , ③
解得:a=2 ![]() ,b=
,b= ![]() ,
,
∴椭圆的标准方程: ![]() ;
;
(Ⅱ)设直线l:x=ty+1,E(x1 , y1),F(x2 , y2),
易知:t=0时,不满足,故t≠0,
则 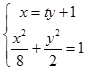 ,整理得:(t2+4)y2+2ty﹣7=0,
,整理得:(t2+4)y2+2ty﹣7=0,
显然△=4t2+28(t2+4)>0,
∴y1+y2=﹣ ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
于是x1+x2=t(y1+y2)+2= ![]() ,
,
故EF的中点D( ![]() ,﹣
,﹣ ![]() ),
),
由△EFG为等边三角形,则丨GE丨=丨GF丨,
连接GD,则kGDkEF=﹣1,
即 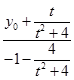 =﹣1,整理得y0=t+
=﹣1,整理得y0=t+ ![]() ,
,
则G(﹣1,t+ ![]() ),
),
由△EFG为等比三角形,则丨GD丨= ![]() 丨EF丨,丨GD丨2=
丨EF丨,丨GD丨2= ![]() 丨EF丨2 ,
丨EF丨2 ,
∴( ![]() +1)2+(t+
+1)2+(t+ ![]() )2=
)2= ![]() (1+t2)[(﹣
(1+t2)[(﹣ ![]() )2﹣4×(﹣
)2﹣4×(﹣ ![]() )],
)],
整理得:( ![]() +1)2=
+1)2= ![]() ,
,
即( ![]() )2=
)2= ![]() ,解得:t2=10,则t=±
,解得:t2=10,则t=± ![]() ,
,
∴直线l的方程x=± ![]() y+1,即y=±
y+1,即y=± ![]() (x﹣1).
(x﹣1).
直线l的方程y=± ![]() (x﹣1).
(x﹣1).
【解析】(Ⅰ)利用椭圆的离心率,椭圆的通径公式,及a2=b2+c2及可求得a和b的值,求得椭圆方程;(Ⅱ)设直线l的方程,代入椭圆方程,根据韦达定理及中点坐标公式求得D点坐标,根据等边三角形的性质,求得G点坐标,由丨GD丨= ![]() 丨EF丨,即可取得t的值,即可求得直线l的方程.
丨EF丨,即可取得t的值,即可求得直线l的方程.
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).


科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品.已知生产一吨甲产品、一吨乙产品所需要的煤、电以及产值如表所示;又知道国家每天分配给该厂的煤和电力有限制,每天供煤至多56吨,供电至多45千瓦.问该厂如何安排生产,才能使该厂日产值最大?最大的产值是多少?
用煤(吨) | 用电(千瓦) | 产值(万元) | |
生产一吨 甲种产品 | 7 | 2 | 8 |
生产一吨 乙种产品 | 3 | 5 | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线E:x2=4y的焦点,直线l为准线,C为抛物线上的一点(C在第一象限),以点C为圆心,|CF|为半径的圆与y轴交于D,F两点,且△CDF为正三角形. 
(Ⅰ)求圆C的方程;
(Ⅱ)设P为l上任意一点,过P作抛物线x2=4y的切线,切点为A,B,判断直线AB与圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
![]() 若
若![]() ,函数在
,函数在![]() 上的最小值为4,求a的值;
上的最小值为4,求a的值;
![]() 对于
对于![]() 中的函数在区间A上的值域是
中的函数在区间A上的值域是![]() ,求区间长度最大的
,求区间长度最大的![]() 注:区间长度
注:区间长度![]() 区间的右端点
区间的右端点![]() 区间的左断点
区间的左断点![]() ;
;
![]() 若
若![]() 中函数的定义域是
中函数的定义域是![]() 解不等式
解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中A,B,C所对的边分别为a,b,c, ![]() (1﹣cos2B)=8sinBsinC,A+
(1﹣cos2B)=8sinBsinC,A+ ![]() =π.
=π.
(Ⅰ)求cosB的值;
(Ⅱ)若点D在线段BC上,且BD=6,c=5,求△ADC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,其准线与
,其准线与![]() 轴交于点
轴交于点![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() 两点,弦
两点,弦![]() 的中点为
的中点为![]() 的垂直平分线与
的垂直平分线与![]() 轴交于
轴交于![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com