
| A. | f(cosA)>f(cosB) | B. | f(sinA)>f(sinB) | C. | f(sinA)>f(cosB) | D. | f(sinA)<f(cosB) |
分析 由C的范围确定出A+B的范围,得到A<$\frac{π}{2}$-B,利用正弦或余弦函数的单调性及f(x)在[0,1]上为单调递减函数,判断即可得到结果.
解答 解:∵在△ABC中,C>$\frac{π}{2}$,
∴0<A+B<$\frac{π}{2}$,即A与B都为锐角,且A<$\frac{π}{2}$-B,
则有sinA<sin($\frac{π}{2}$-B)=cosB,cosA>cos($\frac{π}{2}$-B)=sinB,
∵函数y=f(x)在[0,1]上为单调递减函数,
∴f(sinA)>f(cosB),f(cosA)<f(sinB),
故选:C.
点评 此题考查了函数单调性的性质,诱导公式,以及正弦、余弦函数的单调性,熟练掌握函数单调性的性质是解本题的关键.


科目:高中数学 来源: 题型:填空题
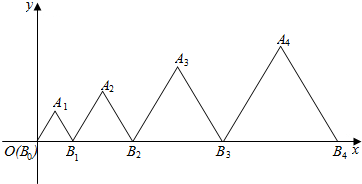 如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则$\frac{a}{d}$的值为1.
如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则$\frac{a}{d}$的值为1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com