
【题目】(2015![]() 新课标II)已知椭圆C:9x2+y2=m2(m
新课标II)已知椭圆C:9x2+y2=m2(m![]() 0),直线l不过原点O且不平行于坐轴,l与C有两个交点A,B,线段AB的中点为M.
0),直线l不过原点O且不平行于坐轴,l与C有两个交点A,B,线段AB的中点为M.
(1)(I)证明:直线OM的斜率与l的斜率的乘积为定值;
(2)(II)若l过点(![]() ,m)延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率,若不能,说明理由.
,m)延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率,若不能,说明理由.
【答案】
(1)
【证明】设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xm,ym)
将y=kx+b代入9x2+y2=m2得(k2+9)x2+2kbx+b2-m2=0,故xM=![]() =
=![]() ,yM=KXM+b=
,yM=KXM+b=![]() ,于是直线OM的斜率KOM=
,于是直线OM的斜率KOM=![]() =-
=-![]() ,即KOM
,即KOM![]() k=-9,所以直线OM的斜率与l的斜率乘积为定值。
k=-9,所以直线OM的斜率与l的斜率乘积为定值。
(2)
当l的斜率为4-![]() 或4+
或4+![]() 时,四边形OAPB为平行四边形
时,四边形OAPB为平行四边形
【解析】(II)四边形OAPB能为平行四边形
因为直线l过点(![]() ,m),所以l不过原点且与C又两个交点的充要条件是k
,m),所以l不过原点且与C又两个交点的充要条件是k![]() 0,k≠3
0,k≠3
由(I)得OM的方程为y=-![]() x,设点P的横坐标为xP
x,设点P的横坐标为xP
由 得
得![]() =
=![]() 即
即![]() =
=![]() ,将点(
,将点(![]() ,m)的坐标代入直线l的方程得b=
,m)的坐标代入直线l的方程得b=![]() ,因此
,因此![]() ,四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分,即
,四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分,即![]() =2
=2![]() 。
。
于是![]() =2x
=2x![]() .解得k1=4-
.解得k1=4-![]() ,k2=4+
,k2=4+![]()
因为ki![]() 0,ki≠3,i=1,2.所以当l的斜率为4-
0,ki≠3,i=1,2.所以当l的斜率为4-![]() 或4+
或4+![]() 时,四边形OAPB为平行四边形.
时,四边形OAPB为平行四边形.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】中国“一带一路”战略构思提出后, 某科技企业为抓住“一带一路”带来的机遇, 决定开发生产一款大型电子设备, 生产这种设备的年固定成本为![]() 万元, 每生产
万元, 每生产![]() 台,需另投入成本
台,需另投入成本![]() (万元), 当年产量不足
(万元), 当年产量不足![]() 台时,
台时,![]() (万元); 当年产量不小于
(万元); 当年产量不小于![]() 台时
台时![]() (万元), 若每台设备售价为
(万元), 若每台设备售价为![]() 万元, 通过市场分析,该企业生产的电子设备能全部售完.
万元, 通过市场分析,该企业生产的电子设备能全部售完.
(1)求年利润![]() (万元)关于年产量
(万元)关于年产量![]() (台)的函数关系式;
(台)的函数关系式;
(2)年产量为多少台时 ,该企业在这一电子设备的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+ax﹣ ![]() (a∈R)在x=2处的切线经过点(﹣4,2ln2)
(a∈R)在x=2处的切线经过点(﹣4,2ln2)
(1)讨论函数f(x)的单调性
(2)若不等式 ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面![]() 与此长方体的面相交,交线围成一个正方形。
与此长方体的面相交,交线围成一个正方形。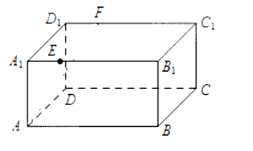
(1)(I)在图中画出这个正方形(不必说明画法与理由);
(2)(II)求平面 把该长方体分成的两部分体积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(2015·新课标Ⅱ)设函数f‘(x)是奇函数f(x)(x![]() R)的导函数,f(-1)=0,当x
R)的导函数,f(-1)=0,当x![]() 0时,xf'(x)-f(x)
0时,xf'(x)-f(x)![]() 0,则使得f(x)
0,则使得f(x)![]() 0成立的x的取值范围是()
0成立的x的取值范围是()
A.(-![]() ,-1)
,-1)![]() (0,1)
(0,1)
B.(-1,0)![]() (1,+
(1,+![]() )
)
C.(-![]() ,-1)
,-1)![]() (-1,0)
(-1,0)
D.(0,1)![]() (1,+
(1,+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)已知函数f(x)=x3+ax+![]() , g(x)=-lnx.
, g(x)=-lnx.
(1)当a为何值时,x轴为曲线y=f(x)的切线;
(2)用min{m,n} 表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(x>0),,讨论h(x)零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.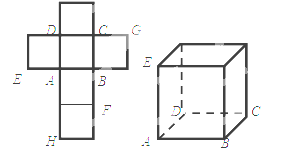
(1)请按字母F , G , H标记在正方体相应地顶点处(不需要说明理由)
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论.
(3)证明:直线DF⊥平面BEG
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)设数列{an}的前n项和为Sn , 已知a1=1, a2=2,且an+1=3Sn-Sn+1+3(n![]() )
)
(1)证明:an+2=3an;
(2)求Sn
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com