
| 与教育有关 | 与教育无关 | 合计 | |
| 男 | 30 | 10 | 40 |
| 女 | 35 | 5 | 40 |
| 合计 | 65 | 15 | 80 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
分析 (1)利用k2计算公式即可得出.
(2)由图表知这80位师范类毕业生从事与教育有关工作的频率.
(3)由题意知X服从$B({4,\frac{13}{16}})$,即可得出E(X).
解答 解:(1)由题意得k2=$\frac{80×(30×5-35×10)^{2}}{40×40×65×15}$=$\frac{80}{39}$<3.841.
故不能在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”
(2)由图表知这80位师范类毕业生从事与教育有关工作的频率$p=\frac{65}{80}=\frac{13}{16}$.
(3)由题意知X服从$B({4,\frac{13}{16}})$,则$EX=np=4×\frac{13}{16}=\frac{13}{4}$.
点评 本题考查了独立性检验原理、二项分布列及其数学期望,考查了推理能力与计算能力,属于中档题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 68 | 75 | 81 | 89 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}+8\sqrt{3}sin(B+\frac{π}{6})$ | B. | $4\sqrt{3}+8sin(B+\frac{π}{3})$ | C. | $4\sqrt{3}+8\sqrt{3}cos(B+\frac{π}{6})$ | D. | $4\sqrt{3}+8cos(B+\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9600}$ | B. | $\frac{1}{18000}$ | C. | $\frac{1}{4500}$ | D. | $\frac{1}{10800}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
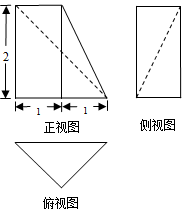
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在${x_0}∈R,{2^{x_0}}>0$ | B. | ?x∈R,2x>0 | ||
| C. | $?{x_0}∈R,{2^{x_0}}≥0$. | D. | ?x∈R,2x≤0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com