
【题目】继空气净化器之后,某商品成为人们抗雾霾的有力手段,根据该商品厂提供的数据,从2015年到2018年,购买该商品的人数直线上升,根据统计图, 说法错误的是( )
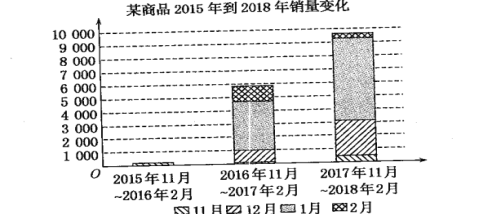
A. 连续3年,该商品在1月的销售量增长显著。
B. 2017年11月到2018年2月销量最多。
C. 从统计图上可以看出,2017年该商品总销量不超过6000台。
D. 2018年2月比2017年2月该商品总销量少。
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆
是椭圆![]() 的一个顶点,且椭圆N的离心率为
的一个顶点,且椭圆N的离心率为![]() .
.
(1)求椭圆N的方程;
(2)已知![]() 是椭圆N的左焦点,过
是椭圆N的左焦点,过![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() 交椭圆N于
交椭圆N于![]() 两点,
两点,![]() 交椭圆N于
交椭圆N于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点是
的焦点是![]() ,直线
,直线![]() :
:![]() ,
,![]() :
:![]() 分别与抛物线
分别与抛物线![]() 相交于点
相交于点![]() 和点
和点![]() ,过
,过![]() ,
,![]() 的直线与圆
的直线与圆![]() :
:![]() 相切.
相切.

(1)求直线![]() 的方程(含
的方程(含![]() 、
、![]() );
);
(2)若线段![]() 与圆
与圆![]() 交于点
交于点![]() ,线段
,线段![]() 与圆
与圆![]() 交于点
交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(如图(1))和女生身高情况的频率分布直方图(如图(2)).已知图(1)中身高在170~175cm的男生有16名.
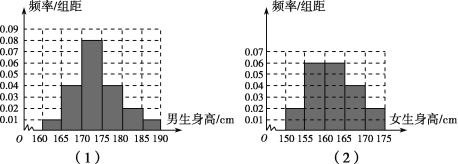
(1)试问在抽取的学生中,男、女生各有多少名?
身高≥170cm | 身高<170cm | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)根据频率分布直方图,完成下面的2×2列联表,并判断能有多大(百分数)的把握认为身高与性别有关?
附:参考公式和临界值表
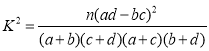
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 过点
过点![]() ,焦点
,焦点![]() ,圆
,圆![]() 的直径为
的直径为![]() .
.
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
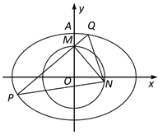
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() )的上顶点为
)的上顶点为![]() ,圆
,圆![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交圆
交圆![]() 于另一点
于另一点![]() .若△PQN的面积为3,求直线
.若△PQN的面积为3,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的数据作了初步处理,得到下面的散点图及一些统计量的值.
y(微克)
 x(千克)
x(千克)
|
|
|
|
|
|
|
3 | 38 | 11 | 10 | 374 | -121 | -751 |
其中![]()
(I)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为蔬菜农药残量
,哪一个适宜作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)若用解析式![]()
![]() 与用水量
与用水量![]() 的回归方程,求出
的回归方程,求出![]() 与
与![]() 的回归方程.(c,d精确到0.1)
的回归方程.(c,d精确到0.1)
(Ⅲ)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时对人体无害,为了放心食用该蔬菜,请估计需要用多少千克的清水清洗一千克蔬菜?(精确到0.1,参考数据![]() )
)
附:参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一年之计在于春,一日之计在于晨,春天是播种的季节,是希望的开端.某种植户对一块地的![]() 个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为
个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为![]() ,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
(1)当![]() 取何值时,有3个坑要补播种的概率最大?最大概率为多少?
取何值时,有3个坑要补播种的概率最大?最大概率为多少?
(2)当![]() 时,用
时,用![]() 表示要补播种的坑的个数,求
表示要补播种的坑的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com