
【题目】已知cosα= ![]() ,cos(αβ)=
,cos(αβ)= ![]() ,且0<β<α<
,且0<β<α< ![]() ,
,
(1)求tan2α的值;
(2)求β.
【答案】
(1)解:由cosα= ![]() ,0<β<α<
,0<β<α< ![]() ,可得sinα=
,可得sinα= ![]() =
= ![]() ,tanα=
,tanα= ![]() =4
=4 ![]() ,
,
∴tan2α= ![]() =
= ![]() =
= ![]() .
.
(2)解:由cosα= ![]() ,cos(αβ)=
,cos(αβ)= ![]() ,且0<β<α<
,且0<β<α< ![]() ,可得sin(αβ)=
,可得sin(αβ)= ![]() =
= ![]() ,
,
∴cosβ=cos[α(αβ)]=cosαcos(αβ)+sinαsin(αβ)
= ![]() +
+ ![]() =
= ![]() ,
,
∴β= ![]() .
.
【解析】(1)由条件利用同角三角函数的基本关系,求得tanα的值,再利用二倍角的正切公式求得tan2α的值.(2)由条件求得sin(αβ)的值,利用两角差的余弦公式求得cosβ=cos[α(αβ)]的值,从而求得β的值.
【考点精析】本题主要考查了同角三角函数基本关系的运用和两角和与差的正切公式的相关知识点,需要掌握同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() ;两角和与差的正切公式:
;两角和与差的正切公式:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图. 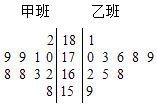
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某厂的产量x与成本y的一组数据:
产量x(千件) | 2 | 3 | 5 | 6 |
成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)根据表中数据,求出回归直线的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 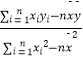 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)预计产量为8千件时的成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,所有正确的序号有( )
①在同一坐标系中,函数y=2x与函数y=log2x的图象关于直线y=x对称;
②函数f(x)=ax+1(a>0,且a≠1)的图象经过定点(0,2);
③函数 ![]() 的最大值为1;
的最大值为1;
④任取x∈R,都有3x>2x .
A.①②③④
B.②
C.①②
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a、b、c,且 ![]() ,B=C. (Ⅰ)求cosB的值;
,B=C. (Ⅰ)求cosB的值;
(Ⅱ)设函数f(x)=sin(2x+B),求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com