
【题目】运动健康已成为大家越来越关心的话题,某公司开发的一个类似计步数据库的公众号.手机用户可以通过关注该公众号查看自己每天行走的步数,同时也可以和好友进行运动量的PK和点赞.现从张华的好友中随机选取40人(男、女各20人),记录他们某一天行走的步数,并将数据整理如表:
步数 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 4 | 7 | 6 |
女 | 0 | 3 | 9 | 6 | 2 |
(1)若某人一天行走的步数超过8000步被评定为“积极型”,否则被评定为“懈怠型”,根据题意完成下列2×2列联表,并据此判断能否有90%的把握认为男、女的“评定类型”有差异?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
(2)在张华的这40位好友中,从该天行走的步数不超过5000步的人中随机抽取2人,设抽取的女性有X人,求X=1时的概率.
参考公式与数据:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
【答案】(1)见解析(2)![]()
【解析】
(1)先得2×2列联表,再根据列联表计算K2的观测值,并结合临界值表可得;
(2)用列举法列举出所有基本事件的种数以及X=1包含的基本事件,再根据古典概型的概率公式可得.
(1)由题意可得列联表
积极型 | 懈怠型 | 总计 | |
男 | 13 | 7 | 20 |
女 | 8 | 12 | 20 |
总计 | 21 | 19 |
K2=![]() =
=![]() ≈2.506<2.706,
≈2.506<2.706,
因此,没有90%的把握认为男、女的“评定类型”有差异;
(2)该天行走的步数不超过5000步的人有3男2女共6人,设男生为A、B、C,女生为a,b,c,
A | B | C | a | b | c | |
A | AB | AC | Aa | Ab | Ac | |
B | BC | Ba | Bb | Bc | ||
C | Ca | Cb | Cc | |||
a | ab | ac | ||||
b | bc | |||||
c |
由图表可知:所有的基本事件个数n=15,事件“X=1”包含的基本事件个数N=9,
所以P(X=1)=![]() =
=![]()


科目:高中数学 来源: 题型:
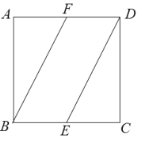
【题目】如图所示,在正方形![]() 中,点
中,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 的中点,将
的中点,将![]() 沿
沿![]() 所在直线进行翻折,将
所在直线进行翻折,将![]() 沿
沿![]() 所在直线进行翻折,在翻折的过程中,
所在直线进行翻折,在翻折的过程中,
①点![]() 与点
与点![]() 在某一位置可能重合;②点
在某一位置可能重合;②点![]() 与点
与点![]() 的最大距离为
的最大距离为![]() ;
;
③直线![]() 与直线
与直线![]() 可能垂直; ④直线
可能垂直; ④直线![]() 与直线
与直线![]() 可能垂直.
可能垂直.
以上说法正确的个数为( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:(1)三角形;(2)长方形;(3)正方形;(4)正六边形.其中正确的结论是____________.(把你认为正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个口袋中装有n个红球(n≥1且n∈N+)和2个白球,从中有放回地连续摸三次,每次摸出2个球,若2个球颜色不同则为中奖,否则不中奖.
(1)当n=3时,设三次摸球中中奖的次数为X,求随机变量X的分布列;
(2)记三次摸球中恰有两次中奖的概率为P,求当n取多少时,P的值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,随着中国第一款5G手机投入市场,5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析,得到如下规律:每生产手机![]() 万台,其总成本为
万台,其总成本为![]() ,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入
,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入![]() 万元满足
万元满足
(1)将利润![]() 表示为产量
表示为产量![]() 万台的函数;
万台的函数;
(2)当产量![]() 为何值时,公司所获利润最大?最大利润为多少万元?
为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在梯形![]() 中,
中,![]() //
//![]() ,且
,且![]() ,
,![]() ,分别延长两腰交于点
,分别延长两腰交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2所示.
,如图2所示.
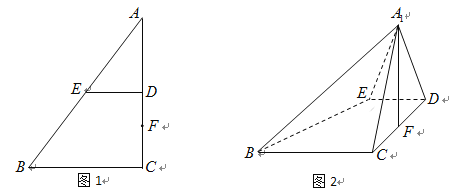
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的表面积.
的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是椭圆
是椭圆![]() 上的两点,已知向量
上的两点,已知向量![]() ,
,![]() ,若
,若![]() 且椭圆的离心率
且椭圆的离心率![]() ,短轴长为2,
,短轴长为2,![]() 为坐标原点.
为坐标原点.
(1)求椭圆的方程;
(2)若直线![]() 过椭圆的焦点
过椭圆的焦点![]() (
(![]() 为半焦距),求直线
为半焦距),求直线![]() 的斜率
的斜率![]() 的值;
的值;
(3)试问:![]() 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系. 直线
轴非负半轴为极轴建立极坐标系. 直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)求圆![]() 的极坐标方程和直线的直角坐标方程;
的极坐标方程和直线的直角坐标方程;
(Ⅱ)射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com