
【题目】函数g(x)=log2 ![]() (x>0),关于方程|g(x)|2+m|g(x)|+2m+3=0有三个不同实数解,则实数m的取值范围为 .
(x>0),关于方程|g(x)|2+m|g(x)|+2m+3=0有三个不同实数解,则实数m的取值范围为 .
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 并且满足2Sn=an2+n,an>0(n∈N*).
(1)求a1 , a2 , a3;
(2)猜想{an}的通项公式,并加以证明;
(3)设x>0,y>0,且x+y=1,证明: ![]() ≤
≤ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图由图中数据可知身高在[120,130]内的学生人数为( )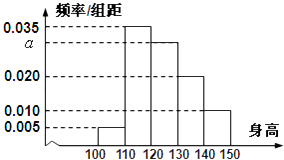
A.20
B.25
C.30
D.35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35
B.0.25
C.0.20
D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“特罗卡”是靶向治疗肺癌的一种药物,为了研究其疗效,医疗专家借助一些肺癌患者,进行人体试验,得到如右丢失一些数据的2×2列联表:
疫苗效果试验列
感染 | 未感染 | 总计 | |
没服用 | 20 | 30 | 50 |
服用 | X | y | 50 |
总计 | M | N | 100 |
设从没服用该药物的肺癌患者中任选两人,未感染人数为ξ;从服用该药物的肺癌患者中任选两人,未感染人数为η,研究人员曾计算过得出:P(ξ=0)= ![]() P(η=0).
P(η=0).
(1)求出列联表中数据x,y,M,N的值.
(2)能否有97.5%的把握认为该药物对治疗肺癌有疗效吗?
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
注:K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)定义在实数集R上的奇函数,当x≥0时,函数y=f(x)的图象如图所示(抛物线的一部分). 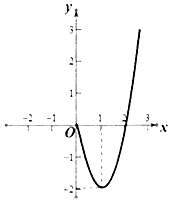
(1)在原图上画出x<0时函数y=f(x)的示意图;
(2)求函数y=f(x)的解析式(不要求写出解题过程);
(3)写出函数y=|f(x)|的单调递增区间(不要求写出解题过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com