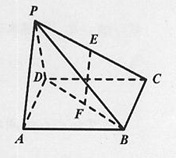
【题目】如图，在四棱锥
中，底面
是边长为2的正方形，
，
分别为
，
的中点，平面
平面，且
.
（1）求证：
平面
；
（2）求三棱锥
的体积.
【答案】（1）详见解析，（2）
【解析】试题分析: （1）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行的寻找与论证，往往需要利用平几知识，如本题分别取
中点，与
构成一个平行四边形，再利用平行四边形性质进行求证；也可连接
，利用三角形中位线性质求证；（2）求三棱锥体积，关键求锥的高，而求锥的高需利用线面垂直关系进行寻找.证明或寻找线面垂直，可结合条件，利用面面垂直性质定理得到
边上中线就是平面
的垂线，最后根据等体积法及椎体体积公式求体积.
试题解析:（1）证明：连接，则
是的中点，
为
的中点，
故在
中，
，
且
平面
，
平面，
∴
平面.
（2）取的中点
，连接
，
∵
，
∴
，
又平面
平面
，平面
平面
，
∴
平面，
∴
.
科目：高中数学 来源： 题型：
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试，现从中随机抽取100人的数学与地理的水平测试成绩如下表：
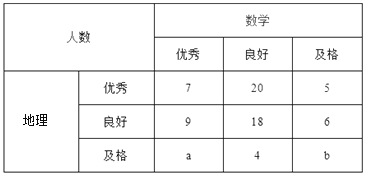
成绩分为优秀、良好、及格三个等级；横向，纵向分别表示地理成绩与数学成绩，例如：表中数学成绩为良好的共有
.
（Ⅰ）若在该样本中，数学成绩优秀率是30％，求
的值；
（Ⅱ）已知
，求数学成绩为优秀的人数比及格的人数少的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f(x)是定义在R上的偶函数，且x≤0时，f(x)＝log
(－x＋1)．
(1)求f(0)，f(1)；
(2)求函数f(x)的解析式；
(3)若f(a－1)<－1，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了研究家用轿车在高速公路上的车速情况，交通部门随机对50名家用轿车驾驶员进行调查，得到其在高速公路上行驶时的平均车速情况为：在30名男性驾驶员中，平均车速超过
的有20人，不超过
的有10人．在20名女性驾驶员中，平均车速超过
的有5人，不超过
的有15人．
（Ⅰ）完成下面的列联表，并判断是否有99.5%的把握认为平均车速超过
的人与性别有关；
平均车速超过
| 平均车速不超过
| 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 |
（Ⅱ ）以上述数据样本来估计总体，现从高速公路上行驶的大量家用轿车中随机抽取3辆，记这3辆车中驾驶员为女性且车速不超过
的车辆数为
，若每次抽取的结果是相互独立的，求
的分布列和数学期望．
参考公式： 
，其中
．
参考数据：
| 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某车间20名工人年龄数据如下表：
年龄（岁） | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数（人） | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
（1）求这20名工人年龄的众数与平均数；
（2）以十位数为茎，个位数为叶，作出这20名工人年龄的茎叶图；
（3）从年龄在24和26的工人中随机抽取2人，求这2人均是24岁的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设A是同时符合以下性质的函数f(x)组成的集合：
①x∈[0，＋∞)，都有f(x)∈(1,4]；②f(x)在[0，＋∞)上是减函数.
(1)判断函数f1(x)＝2－
和f2(x)＝1＋3·
(x≥0)是否属于集合A，并简要说明理由；
(2)把(1)中你认为是集合A中的一个函数记为g(x)，若不等式g(x)＋g(x＋2)≤k对任意的x≥0总成立，求实数k的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】有甲、乙两个班级进行数学考试，按照大于或等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的2×2列联表．已知从全部210人中随机抽取1人为优秀的概率为
.
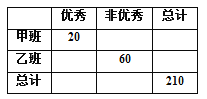
(1)请完成上面的2×2列联表，并判断若按99%的可靠性要求，能否认为“成绩与班级有关”；
(2)从全部210人中有放回地抽取3次，每次抽取1人，记被抽取的3人中的优秀人数为ξ，若每次抽取的结果是相互独立的，求ξ的分布列及数学期望E(ξ)．
P(K2≥k0) | 0.05 | 0.01 |
k0 | 3.841 | 6.635 |
附：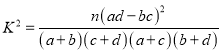 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
