
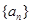 是首项为a,公差为d的等差数列
是首项为a,公差为d的等差数列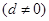 ,
,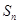 是其前n项的和。记
是其前n项的和。记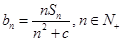 ,其中c为实数。
,其中c为实数。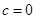 ,且
,且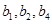 成等比数列,证明:
成等比数列,证明: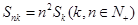 ;
;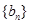 是等差数列,证明:
是等差数列,证明: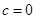 。
。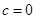 时,可得
时,可得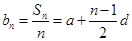 ,即得到
,即得到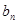 通项,则可根据
通项,则可根据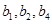 成等比数列,得到
成等比数列,得到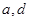 关系,从而将
关系,从而将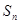 化为关于
化为关于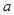 的式子.进而证明结论.
的式子.进而证明结论.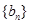 是等差数列,可设出
是等差数列,可设出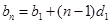 ,则有
,则有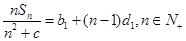 ,将
,将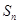 代入,化简该式为
代入,化简该式为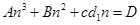 样式,通过令
样式,通过令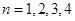 ,建立方程组,可解得
,建立方程组,可解得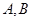 .则可讨论出
.则可讨论出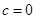 .
.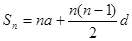 .①
.①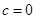 ,得
,得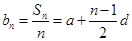 .
.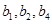 成等比数列,所以
成等比数列,所以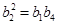 ,
,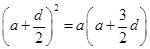 ,化简得
,化简得 .
.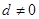 ,所以
,所以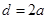 .因此对于所有的
.因此对于所有的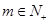 ,①有
,①有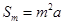 .
.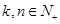 ,有
,有 。
。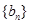 的公差为
的公差为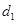 ,则
,则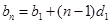 ,
,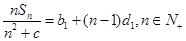 ,代入
,代入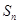 的表达式,整理得,对于所有的
的表达式,整理得,对于所有的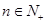 ,
,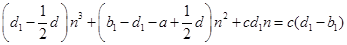 .
.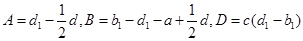 ,
,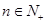 ,有
,有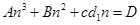 .(*)
.(*)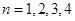 ,得
,得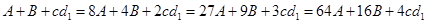 ,
,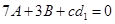 ①,
①,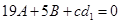 ②,
②,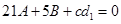 ③,
③,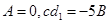 ,代入方程①,得
,代入方程①,得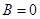 ,从而
,从而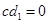 .
.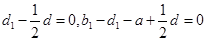 ,
,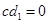 。
。 ,则由
,则由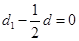 ,得
,得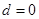 ,与题设矛盾,所以
,与题设矛盾,所以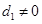 。
。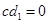 ,所以
,所以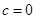 。
。 项和,等比中项;化繁为简的思想,等价代换的思想.
项和,等比中项;化繁为简的思想,等价代换的思想.

科目:高中数学 来源:不详 题型:解答题
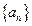 是首项为
是首项为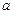 ,公差为
,公差为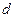 的等差数列(d≠0),
的等差数列(d≠0),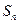 是其前
是其前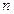 项和.记bn=
项和.记bn=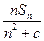 ,
,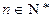 ,其中
,其中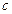 为实数.
为实数. ,且
,且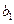 ,
,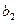 ,
,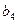 成等比数列,证明:Snk=n2Sk(k,n∈N+);
成等比数列,证明:Snk=n2Sk(k,n∈N+);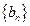 是等差数列,证明:
是等差数列,证明: .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com