
【题目】土壤重金属污染已经成为快速工业化和经济高速增长地区的一个严重问题,污染土壤中的某些重金属易被农作物吸收,并转入食物链影响大众健康.A,B两种重金属作为潜在的致癌物质,应引起特别关注.某中学科技小组对由A,B两种重金属组成的1000克混合物进行研究,测得其体积为100立方厘米(不考虑物理及化学变化),已知重金属A的密度大于![]() ,小于
,小于![]() ,重金属B的密度为
,重金属B的密度为![]() .试计算此混合物中重金属A的克数的范围.
.试计算此混合物中重金属A的克数的范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):

若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望。
的数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 平面ABC,点D,E,F分别为PC,AB,AC的中点.
平面ABC,点D,E,F分别为PC,AB,AC的中点.
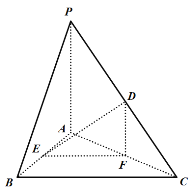
(Ⅰ)求证:![]() 平面DEF;
平面DEF;
(Ⅱ)求证:![]() .
.
阅读下面给出的解答过程及思路分析.
解答:(Ⅰ)证明:在![]() 中,因为E,F分别为AB,AC的中点,所以①.
中,因为E,F分别为AB,AC的中点,所以①.
因为![]() 平面DEF,
平面DEF,![]() 平面DEF,所以
平面DEF,所以![]() 平面DEF.
平面DEF.
(Ⅱ)证明:因为![]() 平面ABC,
平面ABC,![]() 平面ABC,所以②.
平面ABC,所以②.
因为D,F分别为PC,AC的中点,所以![]() .所以
.所以![]() .
.
思路第(Ⅰ)问是先证③,再证“线面平行”;
第(Ⅱ)问是先证④,再证⑤,最后证“线线垂直”.
以上证明过程及思路分析中,设置了①~⑤五个空格,如下的表格中为每个空格给出了三个选项,其中只有一个正确,请选出你认为正确的选项,并填写在答题卡的指定位置.
空格 | 选项 | ||
① | A. | B. | C. |
② | A. | B. | C. |
③ | A.线线垂直 | B.线面垂直 | C.线线平行 |
④ | A.线线垂直 | B.线面垂直 | C.线线平行 |
⑤ | A.线面平行 | B.线线平行 | C.线面垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f(![]() )
)![]() .
.
(Ⅰ)求实数m,n的值,并用定义证明f(x)在(﹣1,1)上是增函数;
(Ⅱ)设函数g(x)是定义在(﹣1,1)上的偶函数,当x∈[0,1)时,g(x)=f(x),求函数g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,点
,点![]() ,直线
,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
,![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,随着中国第一款5G手机投入市场,5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析,得到如下规律:每生产手机![]() 万台,其总成本为
万台,其总成本为![]() ,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入
,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入![]() 万元满足
万元满足
(1)将利润![]() 表示为产量
表示为产量![]() 万台的函数;
万台的函数;
(2)当产量![]() 为何值时,公司所获利润最大?最大利润为多少万元?
为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com