Question

【题目】在直角坐标中xOy，圆C1：x2+y2=8，圆C2：x2+y2=18，点M（1，0），动点A、B分别在圆C1和圆C2上，满足，则的取值范围是______．

Answer 1

【答案】（，）

【解析】

设A（x1，y1）、B（x2，y2），由条件可得|AB|2 =28-2（x1+x2）．设AB中点为N（x0，y0），则|AB|2=28-4x0 ，利用线段的中点公式求得（x0-）2+y02=，再由x0 的范围，求得|AB的范围即可求出的范围.

解：

∵，

∴，

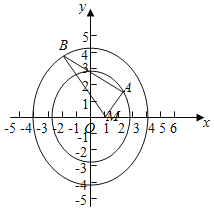
∴A（x1，y1）、B（x2，y2），则|AB|2=（x2-x1）2+（y2-y1）2=26-2（x1x2+y1y2）．

∵-2≤x1≤2，，

∴（x1-1，y1）．（x2-1，y2）=0，即（x1-1）（x2-1）+y1y2=0，即x1x2+y1y2=x1+x2-1，

∴|AB|2=26-2（x1+x2-1）=28-2（x1+x2）．

设AB中点为N（x0，y0），则|AB|2=28-4x0 ，

∵，

∴4（x02+y02）=26+2（x1x2+y1y2）=26+2（x1+x2-1）=24+4x0，即（x0-）2+y02=，

∴点N（x0，y0）的轨迹是以（，0）为圆心、半径等于的圆，

∴x0的取值范围是（-2，3），

∴|AB|2=28-4x0 的范围为（16，36），

则的取值范围为（）

故答案为：（）