
分析 根据函数奇偶性的性质先求出函数的解析式,进行求解即可.
解答 解:∵函数f(x)是定义在R上的奇函数,
∴f(0)=0,
若x>0,则-x<0,则-x<0,则f(-x)=x2-2=-f(x),
即f(x)=-x2+2,x>0,
当x<0时,不等式f(x)<x等价为x2-2<x,即x2-x-2<0,即-1<x<2,此时-1<x<0,
当x>0时,不等式f(x)<x等价为-x2+2<x,即x2+x-2>0,即x>1或x<-2,此时x>1,
当x=0时,不等式不成立,
综上不等式的解为-1<x<0或x>1,
即不等式的解集为(1,+∞)∪(-1,0),
故答案为:(1,+∞)∪(-1,0)
点评 本题主要考查不等式的求解,结合函数奇偶性的性质进行转化求解是解决本题的关键.注意要进行分类讨论.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
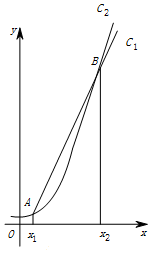 函数f(x)=2x和g(x)=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},则a+b=10.
函数f(x)=2x和g(x)=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},则a+b=10.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
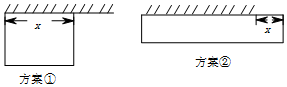 上海市复兴高级中学二期改扩建工程于2015年9月正式开始,现需要围建一个面积火900平方米的矩形地场地的围墙,有一面长度为20米的旧墙(图中斜杠部),有甲、乙两种维修利用旧墙方案.
上海市复兴高级中学二期改扩建工程于2015年9月正式开始,现需要围建一个面积火900平方米的矩形地场地的围墙,有一面长度为20米的旧墙(图中斜杠部),有甲、乙两种维修利用旧墙方案.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)、f(x&2)的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com