
【题目】某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=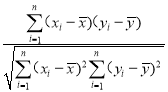 ,
,![]() ≈1.414.
≈1.414.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)详见解析
;(3)详见解析
【解析】
(1)利用野生动物数量的估计值等于样区野生动物平均数乘以地块数,代入数据即可;
(2)利用公式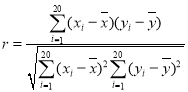 计算即可;
计算即可;
(3)各地块间植物覆盖面积差异较大,为提高样本数据的代表性,应采用分层抽样.
(1)样区野生动物平均数为![]() ,
,
地块数为200,该地区这种野生动物的估计值为![]()
(2)样本![]() (i=1,2,…,20)的相关系数为
(i=1,2,…,20)的相关系数为
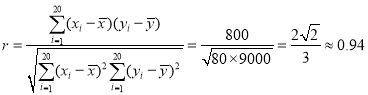
(3)由(2)知各样区的这种野生动物的数量与植物覆盖面积有很强的正相关性,
由于各地块间植物覆盖面积差异很大,从俄各地块间这种野生动物的数量差异很大,
采用分层抽样的方法较好地保持了样本结构与总体结构得以执行,提高了样本的代表性,
从而可以获得该地区这种野生动物数量更准确的估计.
【点晴】
本题主要考查平均数的估计值、相关系数的计算以及抽样方法的选取,考查学生数学运算能力,是一道容易题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
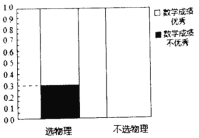
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: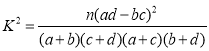
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关线性回归分析的四个命题:
①线性回归直线必过样本数据的中心点(![]() );
);
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于
就越接近于![]() .
.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中盈不足章中有这样一则故事:“今有良马与驽马发长安,至齐. 齐去长安三千里. 良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.” 为了计算每天良马和驽马所走的路程之和,设计框图如下图. 若输出的 ![]() 的值为 350,则判断框中可填( )
的值为 350,则判断框中可填( )
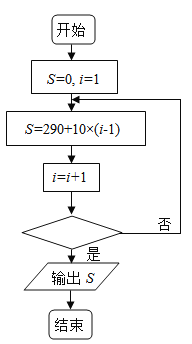
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为![]() ,
,
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l![]() 平面α,直线m⊥平面α,则m⊥l.
平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是__________.
①![]() ②
②![]() ③
③![]() ④
④![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大报告要求,确保到2020年我国现行标准下农村贫困人口实现脱贫,贫困县全部摘帽,解决区域性整体贫困,做到脱真贫、真脱贫.某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领农村地区人民群众脱贫奔小康,扶贫办计划为某农村地区购买农机机器,假设该种机器使用三年后即被淘汰.农机机器制造商对购买该机器的客户推出了两种销售方案:
方案一:每台机器售价7000元,三年内可免费保养2次,超过2次每次收取保养费200元;
方案二:每台机器售价7050元,三年内可免费保养3次,超过3次每次收取保养费100元.
扶贫办需要决策在购买机器时应该选取那种方案,为此搜集并整理了50台这种机器在三年使用期内保养的次数,得下表:
保养次数 | 0 | 1 | 2 | 3 | 4 | 5 |
台数 | 1 | 10 | 19 | 14 | 4 | 2 |
记x表示1台机器在三年使用期内的保养次数.
(1)用样本估计总体的思想,求“x不超过3”的概率;
(2)按照两种销售方案,分别计算这50台机器三年使用期内的总费用(总费用=售价+保养费),以每台每年的平均费用作为决策依据,扶贫办选择那种销售方案购买机器更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过抛物线C:y2=4x的焦点F且与C交于A(x1,y1),B(x2,y2)两点,则y1y2=_____.过A,B两点分别作抛物线C的准线的垂线,垂足分别为P,Q,准线与x轴的交点为M,四边形FAPM的面积记为S1,四边形FBQM的面积记为S2,则S1S2﹣3|AF||BF|=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com