
| A. | $\frac{3}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
分析 分别延长 PA、PB 至A1、B1,使PA1=3PA,PB1=3PB,
利用$\overrightarrow{{PA}_{1}}$+$\overrightarrow{{PB}_{1}}$+$\overrightarrow{PC}$=$\overrightarrow{0}$得点P是三角形 A1B1C的重心,
设△A1B1C的面积为 3S,表示出S△PAC、S△PBC和S△PAB,
即可得出△PAC与△ABC的面积之比.
解答 解:如图所示,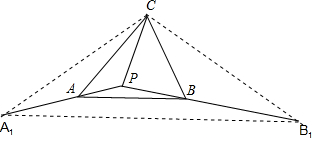
分别延长 PA、PB 至A1、B1,使PA1=3PA,PB1=3PB,
则由$3\overrightarrow{PA}+3\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow 0$
得$\overrightarrow{{PA}_{1}}$+$\overrightarrow{{PB}_{1}}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,
故点P是三角形 A1B1C的重心,
设△A1B1C的面积为 3S,则
${S}_{{△A}_{1}PC}$=${S}_{{△B}_{1}PC}$=${S}_{{{△A}_{1}B}_{1}P}$=S,
S△PAC=$\frac{1}{3}$${S}_{△{PA}_{1}C}$=$\frac{1}{3}$S,
S△PBC=$\frac{1}{3}$${S}_{△{PB}_{1}C}$=$\frac{1}{3}$S,
S△PAB=$\frac{1}{3}$×$\frac{1}{3}$${S}_{△{{PA}_{1}B}_{1}}$=$\frac{1}{9}$S,
所以△PAC与△ABC的面积之比为
$\frac{{S}_{△PAC}}{{S}_{△ABC}}$=$\frac{\frac{1}{3}S}{\frac{1}{3}S+\frac{1}{3}S+\frac{1}{9}S}$=$\frac{3}{7}$.
故选:A.
点评 本题考查了向量的几何意义,作辅助线得出点P是三角形 A1B1 C的重心是解题的关键,属综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,7] | B. | $[{-\frac{1}{2}\;,\;\;2}]$ | C. | [-3,2] | D. | [-1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com