
【题目】已知数列{an}是公差为2的等差数列,且a1 , a4 , a13成等比数列,数列{ ![]() }是首项为1,公比为3的等比数列.
}是首项为1,公比为3的等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)设数列{an+bn}的前n项和Rn , 若不等式 ![]() ≤λ3n+n+3对n∈N*恒成立,求λ的取值范围.
≤λ3n+n+3对n∈N*恒成立,求λ的取值范围.
【答案】
(1)解:依题意得d=2 ![]()
解得a1=3
∴an=a1+(n﹣1)d=3+2(n﹣1)=2n+1,即an=2n+1.
又数列 ![]() 是首项为1,公比为3的等比数列,
是首项为1,公比为3的等比数列,
∴ ![]() ,
,
∴ ![]()
(2)解:令 ![]() ,
,
![]() ,
,
两式相减得: ![]() ,
,
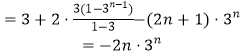 ,
,
∴ ![]()
∴ ![]() ,
,
=n(3n+n+2)
由 ![]() 对n∈N+恒成立可得
对n∈N+恒成立可得 ![]() 对n∈N+恒成立,
对n∈N+恒成立,
则λ≥1
【解析】(1)数列{an}是公差为2的等差数列,a1 , a4 , a13成等比数列,d=2 ![]() 求得a1 , 根据等差数列通项公式即可求得an , 由
求得a1 , 根据等差数列通项公式即可求得an , 由 ![]() ,将an , 的通项公式代入即可求得数列{bn}的通项公式;(2)由(1)可知,利用乘以公比“错位相减法”求得数列{bn}前n项和,求得数列{an}的前n项和,即可求得Rn , 根据式
,将an , 的通项公式代入即可求得数列{bn}的通项公式;(2)由(1)可知,利用乘以公比“错位相减法”求得数列{bn}前n项和,求得数列{an}的前n项和,即可求得Rn , 根据式 ![]() ≤λ3n+n+3,采用分离变量
≤λ3n+n+3,采用分离变量 ![]() ,根据函数的单调性,求λ的取值范围.
,根据函数的单调性,求λ的取值范围.
【考点精析】认真审题,首先需要了解等比数列的通项公式(及其变式)(通项公式:![]() ),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系
),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系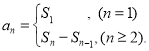 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C= ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在区间![]() 上的函数
上的函数![]() 的图象为
的图象为![]() ,
, ![]() 、
、![]() ,且
,且![]() 为图象
为图象![]() 上的任意一点,
上的任意一点, ![]() 为坐标原点,当实数
为坐标原点,当实数![]() 满足
满足![]() 时,记向量
时,记向量![]() ,若
,若![]() 恒成立,则称函数
恒成立,则称函数![]() 在区间
在区间![]() 上可在标准
上可在标准![]() 下线性近似,其中
下线性近似,其中![]() 是一个确定的正数.
是一个确定的正数.
(1)设函数![]() 在区间
在区间![]() 上可在标准
上可在标准![]() 下线性近似,求
下线性近似,求![]() 的取值范围;
的取值范围;
(2)已知函数![]() 的反函数为
的反函数为![]() ,函数
,函数![]() ,(
,( ![]() ),点
),点![]() 、
、![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,问:是否存在
,问:是否存在![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一块三角形地![]() 的一角
的一角![]() 开辟为水果园,已知角
开辟为水果园,已知角![]() 为
为![]() ,
, ![]() 的长度均大于200米,现在边界
的长度均大于200米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 、
、![]() 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块![]() 面积最大?
面积最大?
(2)已知竹篱笆长为![]() 米,
米, ![]() 段围墙高1米,
段围墙高1米, ![]() 段围墙高2米,造价均为每平方米100元,若
段围墙高2米,造价均为每平方米100元,若![]() ,求围墙总造价的取值范围.
,求围墙总造价的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过点M(﹣1,2)且与以P(﹣2,﹣3),Q(4,0)为端点的线段PQ相交,则l的斜率的取值范围是( )
A.[﹣ ![]() ,5]
,5]
B.[﹣ ![]() ,0)∪(0,5]
,0)∪(0,5]
C.[﹣ ![]() ,
, ![]() )∪(
)∪( ![]() ,5]
,5]
D.(﹣∞,﹣ ![]() ]∪[5,+∞)
]∪[5,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com