
 如图所示,有一边长分别为8与5的长方形,在各角剪去相同的小正方形,把四边折起作成一个无盖小盒,要使纸盒的容积最大,求剪去的小正方形的边长及容积最大值.
如图所示,有一边长分别为8与5的长方形,在各角剪去相同的小正方形,把四边折起作成一个无盖小盒,要使纸盒的容积最大,求剪去的小正方形的边长及容积最大值. 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:设计必修四数学苏教版 苏教版 题型:044
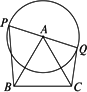
如图所示,△ABC三边长分别为a、b、c,以A为圆心,r为半径作圆,PQ为直径,试判断P、Q在什么位置时,![]() 有最大值?
有最大值?
查看答案和解析>>
科目:高中数学 来源:中华一题 高中数学必修3·B版(配套人民教育出版社实验教科书) 人教版 题型:022
如图所示,在一边长分别为a、b(a>b>0)的矩形内画一个梯形,梯形上、下底分别为![]() a与
a与![]() a,高为b.向该矩形内随机投一点,则所投的点落在梯形内部的概率是________.
a,高为b.向该矩形内随机投一点,则所投的点落在梯形内部的概率是________.

查看答案和解析>>
科目:高中数学 来源:山东省济南世纪英华实验学校2011-2012学年高二下学期期中考试数学理科试题 题型:044
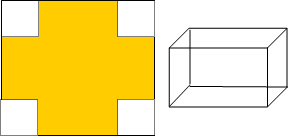
如图所示,现有一边长为6的正方形铁板,如果从铁板的四个角各截出去一个相同的小正方形,做成一个长方体形的无盖容器.为使其容积最大,截下的小正方形边长应为多少?
查看答案和解析>>
科目:高中数学 来源:2013届山东省济南世纪英华实验学校高二下期中理科数学试卷(解析版) 题型:解答题
如图所示,现有一边长为6的正方形铁板,如果从铁板的四个角各截出去一个相同的小正方形,做成一个长方体形的无盖容器为使其容积最大,截下的小正方形边长应为多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com