
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位女教师的概率.
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】昆明市某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300),该社团将该校区在2018年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如图4,把该直方图所得频率估计为概率.
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4度中度污染 | 5度重度污染 | 6级严重污染 |
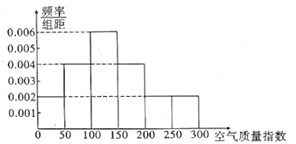
(1)请估算2019年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(2)用分层抽样的方法共抽取10天,则空气质量指数在![]() ,
,![]() ,
,![]() 的天数中各应抽取几天?
的天数中各应抽取几天?
(3)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元若在(2)的条件下,从空气质量指数在![]() 的天数中任意抽取两天,求这两天的净化空气总费用
的天数中任意抽取两天,求这两天的净化空气总费用![]() 的分布列
的分布列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() :
: (
(![]() 为参数)和定点
为参数)和定点![]() ,
,![]() 是曲线
是曲线![]() 的左、右焦点,以原点
的左、右焦点,以原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴且取相同单位长度建立极坐标系.
轴的非负半轴为极轴且取相同单位长度建立极坐标系.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,且
是正方形,且![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
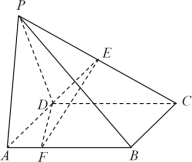
(Ⅰ)求证:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)设二面角![]() 的平面角为
的平面角为![]() ,试判断在线段
,试判断在线段![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 设![]() 是实数,若方程
是实数,若方程![]() 表示双曲线,则
表示双曲线,则![]() .
.
B. “![]() 为真命题”是“
为真命题”是“![]() 为真命题”的充分不必要条件.
为真命题”的充分不必要条件.
C. 命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,
,![]() ”.
”.
D. 命题“若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题是真命题.
”的逆命题是真命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com