
【题目】已知函数f(x)= ![]() +
+ ![]() .
.
(1)求函数f(x)的定义域和值域;
(2)设F(x)= ![]() [f2(x)﹣2]+f(x)(a为实数),求F(x)在a<0时的最大值g(a);
[f2(x)﹣2]+f(x)(a为实数),求F(x)在a<0时的最大值g(a);
(3)对(2)中g(a),若﹣m2+2tm+ ![]() ≤g(a)对a<0所有的实数a及t∈[﹣1,1]恒成立,求实数m的取值范围.
≤g(a)对a<0所有的实数a及t∈[﹣1,1]恒成立,求实数m的取值范围.
【答案】
(1)解:由1+x≥0且1﹣x≥0,得﹣1≤x≤1,
所以函数的定义域为[﹣1,1],
又[f(x)]2=2+2 ![]() ∈[2,4],由f(x)≥0,得f(x)∈[
∈[2,4],由f(x)≥0,得f(x)∈[ ![]() ,2],
,2],
所以函数值域为[ ![]() ,2]
,2]
(2)解:因为F(x)= ![]() =a
=a ![]() +
+ ![]() +
+ ![]() ,
,
令t=f(x)= ![]() +
+ ![]() ,则
,则 ![]() =
= ![]() ﹣1,
﹣1,
∴F(x)=m(t)=a( ![]() ﹣1)+t=
﹣1)+t= ![]() ,t∈[
,t∈[ ![]() ,2],
,2],
由题意知g(a)即为函数m(t)= ![]() ,t∈[
,t∈[ ![]() ,2]的最大值.
,2]的最大值.
注意到直线t=﹣ ![]() 是抛物线m(t)=
是抛物线m(t)= ![]() 的对称轴.
的对称轴.
因为a<0时,函数y=m(t),t∈[ ![]() ,2]的图象是开口向下的抛物线的一段,
,2]的图象是开口向下的抛物线的一段,
①若t=﹣ ![]() ∈(0,
∈(0, ![]() ],即a≤﹣
],即a≤﹣ ![]() ,则g(a)=m(
,则g(a)=m( ![]() )=
)= ![]() ;
;
②若t=﹣ ![]() ∈(
∈( ![]() ,2],即﹣
,2],即﹣ ![]() <a≤﹣
<a≤﹣ ![]() ,则g(a)=m(﹣
,则g(a)=m(﹣ ![]() )=﹣a﹣
)=﹣a﹣ ![]() ;
;
③若t=﹣ ![]() ∈(2,+∞),即﹣
∈(2,+∞),即﹣ ![]() <a<0,则g(a)=m(2)=a+2,
<a<0,则g(a)=m(2)=a+2,
综上有g(a)= 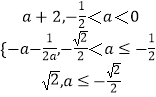
(3)解:易得 ![]() ,
,
由﹣ ![]() ≤g(a)对a<0恒成立,即要使﹣
≤g(a)对a<0恒成立,即要使﹣ ![]() ≤gmin(a)=
≤gmin(a)= ![]() 恒成立,
恒成立,
m2﹣2tm≥0,令h(t)=﹣2mt+m2,对所有的t∈[﹣1,1],h(t)≥0成立,
只需 ![]() ,
,
解得m的取值范围是m≤﹣2或m=0,或m≥2
【解析】(1)由1+x≥0且1﹣x≥0可求得定义域,先求[f(x)]2的值域,再求f(x)的值域;(2)F(x)=a ![]() +
+ ![]() +
+ ![]() ,令t=f(x)=
,令t=f(x)= ![]() +
+ ![]() ,则
,则 ![]() =
= ![]() ﹣1,由此可转化为关于t的二次函数,按照对称轴t=﹣
﹣1,由此可转化为关于t的二次函数,按照对称轴t=﹣ ![]() 与t的范围[
与t的范围[ ![]() ,2]的位置关系分三种情况讨论,借助单调性即可求得其最大值;(3)先由(2)求出函数g(x)的最小值,﹣
,2]的位置关系分三种情况讨论,借助单调性即可求得其最大值;(3)先由(2)求出函数g(x)的最小值,﹣ ![]() ≤g(a)对a<0恒成立,即要使﹣
≤g(a)对a<0恒成立,即要使﹣ ![]() ≤gmin(a)恒成立,从而转化为关于t的一次不等式,再根据一次函数的单调性可得不等式组,解出即可.
≤gmin(a)恒成立,从而转化为关于t的一次不等式,再根据一次函数的单调性可得不等式组,解出即可.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos(θ﹣ ![]() )=1,A,B分别为C与x轴,y轴的交点.
)=1,A,B分别为C与x轴,y轴的交点.
(1)写出C的直角坐标方程,并求A,B的极坐标;
(2)设M为曲线C上的一个动点, ![]() =λ
=λ ![]() (λ>0),|
(λ>0),| ![]() ||
|| ![]() |=2,求动点Q的极坐标方程.
|=2,求动点Q的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() ,焦点
,焦点![]() ,
, ![]() 为坐标原点,直线
为坐标原点,直线![]() (不垂直
(不垂直![]() 轴)过点
轴)过点![]() 且与抛物线
且与抛物线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若![]() 为线段
为线段![]() 的中点,射线
的中点,射线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人进行羽毛球练习赛,其中两人比赛另一个人当裁判,设每周比赛结束时,负的一方在下一局当裁判,假设每局比赛中甲胜乙的概率为![]() ,甲胜丙,乙胜丙的概率都是
,甲胜丙,乙胜丙的概率都是![]() ,各局的比赛相互独立,第一局甲当裁判.
,各局的比赛相互独立,第一局甲当裁判.
(1)求第三局甲当裁判的概率;
(2)记前四次中乙当裁判的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (其中常数a>0,且a≠1).
(其中常数a>0,且a≠1).
(1)当a=10时,解关于x的方程f(x)=m(其中常数m>2 ![]() );
);
(2)若函数f(x)在(﹣∞,2]上的最小值是一个与a无关的常数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,外接球的球心为
,外接球的球心为![]() ,点
,点![]() 是侧棱
是侧棱![]() 上的一个动点.有下列判断:
上的一个动点.有下列判断:
① 直线![]() 与直线
与直线![]() 是异面直线;②
是异面直线;② ![]() 一定不垂直
一定不垂直![]() ;
;
③ 三棱锥![]() 的体积为定值; ④
的体积为定值; ④![]() 的最小值为
的最小值为![]() .
.

其中正确的个数是
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com