
【题目】已知![]() 为常数,
为常数, ![]() ,函数
,函数![]() ,
,![]() 且方程
且方程![]() 有等
有等
根.
(1)求![]() 的解析式及值域;
的解析式及值域;
(2)设集合![]() ,
,![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使
,使![]() 的定义域和值域分别为
的定义域和值域分别为![]() 和
和![]() ?若存在,求
?若存在,求
出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】设命题p:x∈[1,2], ![]() ﹣lnx﹣a≥0,命题q:x0∈R,使得x02+2ax0﹣8﹣6a≤0,如果命题“p或q”是真命题,命题“p且q”是假命题,求实数a的取值范围.
﹣lnx﹣a≥0,命题q:x0∈R,使得x02+2ax0﹣8﹣6a≤0,如果命题“p或q”是真命题,命题“p且q”是假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有A、B两家羽毛球球俱乐部,两家设备和服务都很好,但收费方式不同,A俱乐部每块场地每小时收费6元;B俱乐部按月计费,一个月中20小时以内![]() 含20小时
含20小时![]() 每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
![]() 设在A俱乐部租一块场地开展活动x小时的收费为
设在A俱乐部租一块场地开展活动x小时的收费为![]() 元
元![]() ,在B俱乐部租一块场地开展活动x小时的收费为
,在B俱乐部租一块场地开展活动x小时的收费为![]() 元
元![]() ,试求
,试求![]() 与
与![]() 的解析式;
的解析式;
![]() 问该企业选择哪家俱乐部比较合算,为什么?
问该企业选择哪家俱乐部比较合算,为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
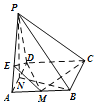
【题目】如图,四棱锥![]() 的底面ABCD是正方形,
的底面ABCD是正方形,![]() 为等边三角形,M,N分别是AB,AD的中点,且平面
为等边三角形,M,N分别是AB,AD的中点,且平面![]() 平面ABCD.
平面ABCD.
![]() 证明:
证明:![]() 平面PNB;
平面PNB;
![]() 设点E是棱PA上一点,若
设点E是棱PA上一点,若![]() 平面DEM,求
平面DEM,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-7x+6<0},B={x|4-t<x<t},R为实数集.
(1)当t=4时,求A∪B及A∩RB;
(2)若A∪B=A,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)求![]() 的值;
的值;
(2)求函数![]() 的极小值;
的极小值;
(3)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)设不等式(x﹣a)(x+a﹣2)<0的解集为N, ![]() ,若x∈N是x∈M的必要条件,求a的取值范围.
,若x∈N是x∈M的必要条件,求a的取值范围.
(2)已知命题:“x∈{x|﹣1<x<1},使等式x2﹣x﹣m=0成立”是真命题,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com