
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 与
与![]() 交于点
交于点![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本题满分12分)如图, ![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() 的点,
的点, ![]() 垂直于圆
垂直于圆![]() 所在的平面,且
所在的平面,且![]() .
.
(Ⅰ)若![]() 为线段
为线段![]() 的中点,求证
的中点,求证![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 体积的最大值;
体积的最大值;
(Ⅲ)若![]() ,点
,点![]() 在线段
在线段![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆N与圆M关于直线
,圆N与圆M关于直线![]() 对称.
对称.
(1)求圆N的方程.
(2)是否存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,使得
,使得![]() 被圆M截得的弦长与
被圆M截得的弦长与![]() 被圆N截得的弦长相等?若存在,求出点P的坐标;若不存在,请说明理由.
被圆N截得的弦长相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设正数数列![]() 的前
的前![]() 项和为
项和为![]() ,对于任意
,对于任意![]() ,
,![]() 是
是![]() 和
和![]() 的等差中项.
的等差中项.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设 ,
,![]() 是
是![]() 的前
的前![]() 项和,是否存在常数
项和,是否存在常数![]() ,对任意
,对任意![]() ,使
,使![]() 恒成立?若存在,求
恒成立?若存在,求![]() 取值范围;若不存在,说明理由.
取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在第十五次全国国民阅读调查中,某地区调查组获得一个容量为![]() 的样本,其中城镇居民
的样本,其中城镇居民![]() 人,农村居民
人,农村居民![]() 人.在这些居民中,经常阅读的城镇居民
人.在这些居民中,经常阅读的城镇居民![]() 人,农村居民
人,农村居民![]() 人.
人.
(Ⅰ)填写下面列联表,并判断是否有![]() 的把握认为,经常阅读与居民居住地有关?
的把握认为,经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 |
|
| |
不经常阅读 | |||
合计 |
|
(Ⅱ)从该地区居民城镇的居民中,随机抽取![]() 位居民参加一次阅读交流活动,记这
位居民参加一次阅读交流活动,记这![]() 位居民中经常阅读的人数为
位居民中经常阅读的人数为![]() ,若用样本的频率作为概率,求随机变量
,若用样本的频率作为概率,求随机变量![]() 的分布列和期望.
的分布列和期望.
附: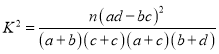 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产某种产品,一条流水线年产量为![]() 件,该生产线分为两段,流水线第一段生产的半成品的质量指标会影响第二段生产成品的等级,具体见下表:
件,该生产线分为两段,流水线第一段生产的半成品的质量指标会影响第二段生产成品的等级,具体见下表:
第一段生产的半成品质量指标 |
|
|
|
第二段生产的成品为一等品概率 | 0.2 | 0.4 | 0.6 |
第二段生产的成品为二等品概率 | 0.3 | 0.3 | 0.3 |
第二段生产的成品为三等品概率 | 0.5 | 0.3 | 0.1 |
从第一道生产工序抽样调查了![]() 件,得到频率分布直方图如图:
件,得到频率分布直方图如图:

若生产一件一等品、二等品、三等品的利润分别是![]() 元、
元、![]() 元、
元、![]() 元.
元.
(Ⅰ)以各组的中间值估计为该组半成品的质量指标,估算流水线第一段生产的半成品质量指标的平均值;
(Ⅱ)将频率估计为概率,试估算一条流水线一年能为该公司创造的利润;
(Ⅲ)现在市面上有一种设备可以安装到流水线第一段,价格是![]() 万元,使用寿命是
万元,使用寿命是![]() 年,安装这种设备后,流水线第一段半成品的质量指标服从正态分布
年,安装这种设备后,流水线第一段半成品的质量指标服从正态分布![]() ,且不影响产量.请你帮该公司作出决策,是否要购买该设备?说明理由.
,且不影响产量.请你帮该公司作出决策,是否要购买该设备?说明理由.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com