
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的圆心为
的圆心为![]() .已知点
.已知点![]() ,且
,且![]() 为圆
为圆![]() 上的动点,线段
上的动点,线段![]() 的中垂线交
的中垂线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,若四边形
,若四边形![]() 的四个顶点都在曲线
的四个顶点都在曲线![]() 上,对角线
上,对角线![]() ,
,![]() 互相垂直并且它们的交点恰为点
互相垂直并且它们的交点恰为点![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
科目:高中数学 来源: 题型:
【题目】蝴蝶定理因其美妙的构图,像是一只翩翩起舞的蝴蝶,一代代数学名家蜂拥而证,正所谓花若芬芳蜂蝶自来.如图,已知圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() .原点
.原点![]() 在圆
在圆![]() 内.
内.

(1)求证:![]() .
.
(2)设![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
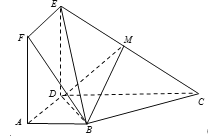
【题目】如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直, ![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ) 若点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求证:平面![]() 平面
平面![]() ;
;
(Ⅲ) 当平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了![]() 年下半年该市
年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工月工资的中位数为
名农民工月工资的中位数为![]() 百元(假设这
百元(假设这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内)且月工资收入在
(百元)内)且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:

(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名,则能否在犯错误的概率不超过
名,则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一楼房高![]() 为
为![]() 米,某广告公司在楼顶安装一块宽
米,某广告公司在楼顶安装一块宽![]() 为
为![]() 米的广告牌,
米的广告牌,![]() 为拉杆,广告牌的倾角为
为拉杆,广告牌的倾角为![]() ,安装过程中,一身高为
,安装过程中,一身高为![]() 米的监理人员
米的监理人员![]() 站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设
站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设![]() 米,该监理人员观察广告牌的视角
米,该监理人员观察广告牌的视角![]() .
.

(1)试将![]() 表示为
表示为![]() 的函数;
的函数;
(2)求点![]() 的位置,使
的位置,使![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在十九大“建设美丽中国”的号召下,某省级生态农业示范县大力实施绿色生产方案,对某种农产品的生产方式分别进行了甲、乙两种方案的改良。为了检查甲、乙两种方案的改良效果,随机在这两种方案中各任意抽取了40件产品作为样本逐件称出它们的重量(单位:克),重量值落在![]() 之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
产品重量 | 甲方案频数 | 乙方案频数 |
| 6 | 2 |
| 8 | 12 |
| 14 | 18 |
| 8 | 6 |
| 4 | 2 |
(1)根据上表数据求甲(同组中的重量值用组中点数值代替)方案样本中40件产品的平均数和中位数
(2)由以上统计数据完成下面![]() 列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
甲方案 | 乙方案 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
参考公式:![]() ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.814 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com