
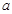 和
和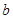 组成数对(
组成数对(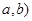 ,并构成函数
,并构成函数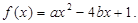
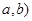 ,并计算
,并计算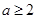 ,且
,且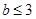 的概率;
的概率;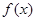 在区间[
在区间[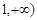 上是增函数的概率.
上是增函数的概率. ;
;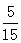 =
=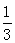 。
。 ……5分
……5分 ……7分
……7分 ≤1即2b≤a. ……9分
≤1即2b≤a. ……9分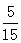 =
=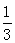 ……11分
……11分

科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
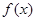 的边际函数
的边际函数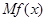 定义为
定义为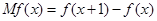 .某公司每月最多生产100台报警系统装置,生产
.某公司每月最多生产100台报警系统装置,生产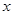 台(
台(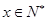 )的收入函数为
)的收入函数为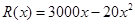 (单位:元),其成本函数为
(单位:元),其成本函数为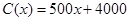 (单位:元),利润是收入与成本之差.
(单位:元),利润是收入与成本之差.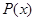 及边际利润函数
及边际利润函数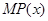 的解析式,并指出它们的定义域;
的解析式,并指出它们的定义域;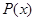 与边际利润函数
与边际利润函数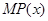 是否具有相同的最大值?说明理由;
是否具有相同的最大值?说明理由; 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com