
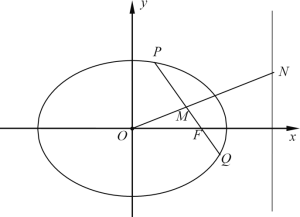
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,其右焦点为
,其右焦点为![]() .点
.点![]() 是椭圆
是椭圆![]() 上异于长轴端点的任意一点,连接
上异于长轴端点的任意一点,连接![]() 并延长交椭圆
并延长交椭圆![]() 于点
于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且直线
为坐标原点,且直线![]() 与右准线
与右准线![]() 交于点
交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() (2)
(2)![]() 或
或![]() .
.
【解析】
(1)由离心率得出a、b、c的等量关系,再将点A的坐标代入椭圆方程,可求出a、b、c的值,从而得出椭圆C的标准方程;(2)解法1:设点P(x0,y0)(y0≠0),对PF与x轴是否垂直进行分类讨论,在两种情况下求中点M的坐标,写出直线OM的方程,并求出点N的坐标,结合条件MN=2OM以及点P的坐标椭圆C的方程可求出点P的坐标;解法2:对直线PQ与x轴是否垂直进行分类讨论,在第一种情况PQ⊥x轴时,分别求出点M、N的坐标,并对条件MN=2OM进行验证是否满足题意;第二种情况就是直线PQ的斜率存在时,设直线PQ的方程为y=k(x﹣1)(k≠0),将直线PQ的方程与椭圆C的方程联立,列出韦达定理,并求出线段PQ的中点M的坐标,由MN=2ON得出k的值,从而得出点P的坐标.
(1)由题意可知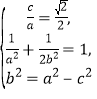 解得
解得![]() ,
,![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)法1:设![]() (
(![]() ).
).
当![]() 时,
时,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,![]() ,不符合题意;
,不符合题意;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 的方程,消去
的方程,消去![]() 整理得
整理得
![]() ,
,
所以![]() 中点
中点![]() 的横坐标
的横坐标![]() ,因为
,因为![]() ,椭圆
,椭圆![]() 的右准线为
的右准线为![]() ,所以
,所以![]() ,从而
,从而![]() ,即
,即![]() . 又因为
. 又因为![]() ,所以
,所以![]() ,解得
,解得![]() 或
或![]() ,故点
,故点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
法2:当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,![]() ,不符合题意;当直线
,不符合题意;当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() :
:![]() ,联立
,联立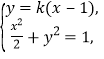 得
得
![]() ,所以
,所以![]() 中点
中点![]() 的横坐标
的横坐标![]() ,因为
,因为![]() ,椭圆
,椭圆![]() 的右准线为
的右准线为![]() ,所以
,所以![]() ,从而
,从而![]() ,解之得
,解之得![]() .当
.当![]() 时,
时,![]() :
:![]() ,联立
,联立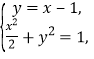 得
得![]() 或
或![]() ;
;
当![]() 时,
时,![]() :
:![]() ,联立
,联立 得
得![]() 或
或![]() .
.
故点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某学生对某小区30位居民的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的,饮食以肉类为主).

(1)根据茎叶图,说明这30位居民中50岁以上的人的饮食习惯;
(2)根据以上数据完成如下2×2列联表;
主食蔬菜 | 主食肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(3)能否有99%的把握认为居民的饮食习惯与年龄有关?
独立性检验的临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月16日下午5时左右,今年第22号台风“山竹”在广东江门川岛镇附近正面登陆,给当地人民造成了巨大的财产损失,某记者调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,并作出如下频率分布直方图.
五组,并作出如下频率分布直方图.
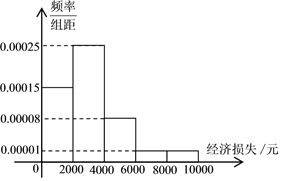
(Ⅰ)根据频率分布直方图估计该小区居民由于台风造成的经济损失的众数和平均值.
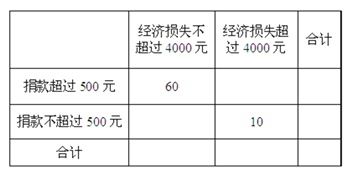
(Ⅱ)“一方有难,八方支援”,台风后居委会号召小区居民为台风重灾区捐款,![]() 记者调查的100户居民捐款情况如下表格,在表格空白处填写正确数字,并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
记者调查的100户居民捐款情况如下表格,在表格空白处填写正确数字,并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
(Ⅲ)将上述调查所得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过![]() 元的人数为
元的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列及期望
的分布列及期望![]() .
.
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体是圆柱的一部分,它是由矩形![]() (及其内部)以
(及其内部)以![]() 边所在直线为旋转轴旋转
边所在直线为旋转轴旋转![]() 得到的,点
得到的,点![]() 是弧
是弧![]() 上的一点,点
上的一点,点![]() 是弧
是弧![]() 的中点.
的中点.
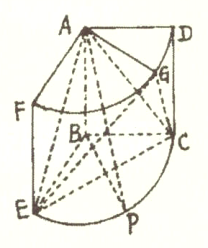
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 且
且![]() 时,求二面角
时,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入![]() (万元)满足
(万元)满足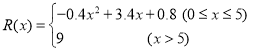 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,完成下列问题:
(1)写出利润函数![]() 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(2)甲厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)若直线![]() 过焦点
过焦点![]() ,且与圆
,且与圆![]() 交于
交于![]() (其中
(其中![]() 在
在![]() 轴同侧),求证:
轴同侧),求证: ![]() 是定值;
是定值;
(Ⅱ)设抛物线![]() 在
在![]() 和
和![]() 点的切线交于点
点的切线交于点![]() ,试问:
,试问: ![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为菱形?若存在,请说明理由并求此时直线
为菱形?若存在,请说明理由并求此时直线![]() 的斜率和点
的斜率和点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校数学与统计学院为了对2018年录取的大一新生有针对性地进行教学.从大一新生中随机抽取40名,对他们在2018年高考的数学成绩进行调查,统计发现40名新生的数学分数![]() 分布在
分布在![]() 内.当
内.当![]() 时,其频率
时,其频率![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)请在答题卡中画出这40名新生高考数学分数的频率分布直方图,并估计这40名新生的高考数学分数的平均数;

(Ⅲ)从成绩在100~120分的学生中,用分层抽样的方法从中抽取5名学生,再从这5名学生中随机选两人甲、乙,记甲、乙的成绩分别为![]() ,求概率
,求概率![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com