②④
分析:①利用三角形两边之差小于第三边可证明当点P在x轴上时,|PF
1|-|PF
2|有最大值2c,由椭圆标准方程计算焦距即可;
②利用椭圆定义知|PF
1|+|PF
2|为定值2a,再利用均值定理求积|PF
1|•|PF
2|的最大值即可;
③利用焦半径公式设P点横坐标为x
0,则|PF
1|
2+|PF
2|
2可转化为关于x0的一元函数,由x
0的范围即可求得|PF
1|
2+|PF
2|
2的最大值;
④由椭圆的定义结合三角形的性质,即可判断
解答:①当P点不在x轴上时,P,F1,F2,三点构成三角形,此时|PF
1|-|PF
2|<|F
1F
2|,
∵|F
1F
2|=4,∴|PF
1|-|PF
2|<4,
当P点在x轴上时,|PF
1|-|PF
2|=|F
1F
2|=4,∴|PF
1|-|PF
2|≤4,即①|PF
1|-|PF
2|有最大值4,①错误.
②∵P点在椭圆
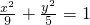
上,∴|PF
1|+|PF
2|=|2a=6,
∵|PF
1|>0,|PF
2|>0,∴|PF
1|•|PF
2|≤
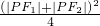
=9,∴|PF
1|•|PF
2|有最大值9,②正确.
③根据椭圆方程,可得椭圆的离心率为

设P点横坐标为x
0,则|PF
1|=a+ex
0,|PF
2|=a-ex
0,
∴|PF
1|
2+|PF
2|
2=(a+ex
0)
2+(a-ex
0)
2=2a
2+2e
2x
02=18+

x
02
∵P点在椭圆
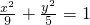
上,∴x
02≤9,∴18+

x
02≤26,∴PF
1|
2+|PF
2|
2有最大值26,
∴③错误,
④由椭圆的定义可知|PF
1|+|PF
2|=2a,,|PF
1|+|PA|+|F
2A|≥|PF
1|+|PF
2|
∴|PF
1|+|PA|≥|PF
1|+|PF
2|-|F
2A|=6-

,所以有最小值
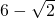
,正确.
故答案为:②④.
点评:本题考查了椭圆的标准方程的意义,椭圆定义的应用,椭圆的几何性质,利用均值定理和函数求最值的方法.

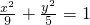 ,F1、F2分别为C的左、右焦点,点A的坐标为(1,1),P是C上的任意一点,给出下列结论:
,F1、F2分别为C的左、右焦点,点A的坐标为(1,1),P是C上的任意一点,给出下列结论: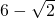 ,其中正确结论的序号是________.
,其中正确结论的序号是________.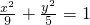 上,∴|PF1|+|PF2|=|2a=6,
上,∴|PF1|+|PF2|=|2a=6,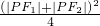 =9,∴|PF1|•|PF2|有最大值9,②正确.
=9,∴|PF1|•|PF2|有最大值9,②正确.
 x02
x02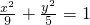 上,∴x02≤9,∴18+
上,∴x02≤9,∴18+ x02≤26,∴PF1|2+|PF2|2有最大值26,
x02≤26,∴PF1|2+|PF2|2有最大值26, ,所以有最小值
,所以有最小值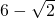 ,正确.
,正确.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案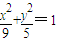 ,F1、F2分别为C的左、右焦点,P是C上的任意一点,给出下列结论:
,F1、F2分别为C的左、右焦点,P是C上的任意一点,给出下列结论: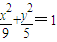 ,F1、F2分别为C的左、右焦点,点A的坐标为(1,1),P是C上的任意一点,给出下列结论:
,F1、F2分别为C的左、右焦点,点A的坐标为(1,1),P是C上的任意一点,给出下列结论: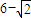 ,其中正确结论的序号是 .
,其中正确结论的序号是 .