
已知数列 中,其中
中,其中 为数列
为数列 的前
的前 项和,并且
项和,并且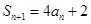 (
( ,
, .
.
(1)设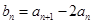 (
( ),求证:数列
),求证:数列 是等比数列;
是等比数列;
(2)设数列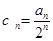 (
( ),求证:数列
),求证:数列 是等差数列;
是等差数列;
(3)求数列 的通项公式和前
的通项公式和前 项.
项.
(1)详见解析;(2)详见解析;(3)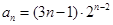 ,
, .
.
解析试题分析:(1)首先条件中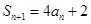 如何处理,通常要归一,即一是转化为相邻三项的关系;二是转化为和之间的关系,这里是转化为相邻三项的关系,接下来根据等比数列的定义,易得数列
如何处理,通常要归一,即一是转化为相邻三项的关系;二是转化为和之间的关系,这里是转化为相邻三项的关系,接下来根据等比数列的定义,易得数列 是等比数列;(2)根据等差数列的定义,结合(1)不难证明数列
是等比数列;(2)根据等差数列的定义,结合(1)不难证明数列 是等比数列;(3)有了(1)(2)的铺垫很容易求得数列
是等比数列;(3)有了(1)(2)的铺垫很容易求得数列 的通项公式,对照通项公式的特点:它是由一个等差数列与一个等比数列对应项相乘得到的,故用错位相减法求数列
的通项公式,对照通项公式的特点:它是由一个等差数列与一个等比数列对应项相乘得到的,故用错位相减法求数列 的
的 .
.
试题解析:(1)证明: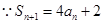 ,
,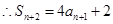 ,两式相减得
,两式相减得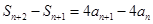 --3分
--3分
即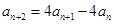 ,变形得
,变形得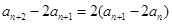
设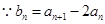 ,则有
,则有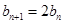 (
( ),又
),又 ,
,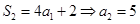 ,
,
从而 ,由此可知,数列
,由此可知,数列 是公比为2的等比数列.
是公比为2的等比数列.
(2)证明:由(1)知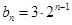
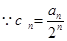 ,
,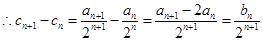
将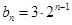 代入得
代入得 (
( )
)
由此可知,数列 是公差为
是公差为 ,首项
,首项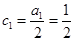 的等差数列,
的等差数列,
故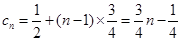 (
( ).
).
(3)由(2)可知: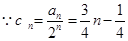 ,
,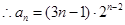
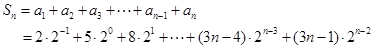
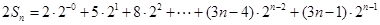
两式错位相减: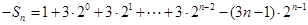
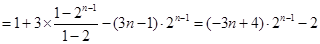
所以
考点:数列中的递推关系式处理及转化数学思想的使用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
在正整数数列中,由1开始依次按如下规则将某些数染成红色:先染1,再染两个偶数2、4;再染4后面最邻近的三个连续奇数5、7、9;再染9后面最邻近的四个连续偶数10、12、14、16;再染此后最邻近的五个连续奇数17、19、21、23、25;按此规则一直染下去,得到一红色子数列1,2,4,5,7,9,10,12,14,16,17,…….则在这个红色子数列中,由1开始的第2011个数是_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com