
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() ,且
,且![]() 是2与
是2与![]() 的等差中项.
的等差中项.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.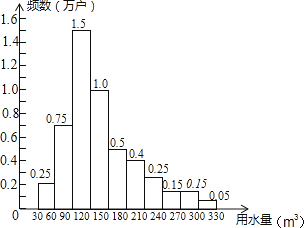
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等边△ABC中,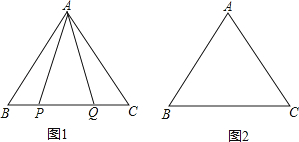
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=a,其前n项和为Sn , 且满足Sn+Sn﹣1=3n2+2n+4(n≥2),若对任意的n∈N* , an<an+1恒成立,则a的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是等差数列,前n项和为Sn , {bn}是单调递增的等比数列,b1=2是a1与a2的等差中项,a3=5,b3=a4+1,若当n≥m时,Sn≤bn恒成立,则m的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考山东文数】已知椭圆C:![]() (a>b>0)的长轴长为4,焦距为2
(a>b>0)的长轴长为4,焦距为2![]() .
.
(I)求椭圆C的方程;
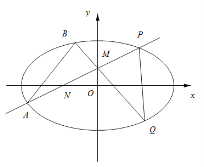
(Ⅱ)过动点M(0,m)(m>0)的直线交x轴与点N,交C于点A,P(P在第一象限),且M是线段PN的中点.过点P作x轴的垂线交C于另一点Q,延长线QM交C于点B.
(i)设直线PM、QM的斜率分别为k、k',证明![]() 为定值.
为定值.
(ii)求直线AB的斜率的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=cos(2x+1)的图象,只要将函数y=cos2x的图象( )
A.向左平移1个单位
B.向右平移1个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)判断函数![]() 在
在![]() 内零点的个数,并说明理由;
内零点的个数,并说明理由;
(Ⅱ)![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com