
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 是椭圆
是椭圆![]() 上的一点,从原点
上的一点,从原点![]() 向圆
向圆![]() 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点![]() .
.
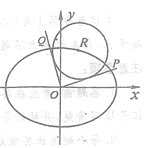
(1)若![]() 点在第一象限,且直线
点在第一象限,且直线![]() 互相垂直,求圆
互相垂直,求圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率存在,并记为
的斜率存在,并记为![]() ,求
,求![]() 的值;
的值;
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,三点
,三点 中恰有二点在椭圆
中恰有二点在椭圆![]() 上,且离心率为
上,且离心率为![]() 。
。

(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为椭圆
为椭圆![]() 的左右顶点,
的左右顶点, ![]() 为
为![]() 中点,求证:直线
中点,求证:直线![]() 与直线
与直线![]() 它们的斜率之积为定值;
它们的斜率之积为定值;
(3)若椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,求证:直线
,求证:直线![]() 与直线
与直线![]() 斜率之和为定值。
斜率之和为定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产部门随机抽测生产某种零件的工人的日加工零件数(单位:件),其中A车间13人,B车间12人,获得数据如下:

根据上述数据得到样本的频率分布表如下:
分组 | 频数 | 频率 |
[25,30] | 3 | 0.12 |
(30,35] | 5 | 0.20 |
(35,40] | 8 | 0.32 |
(40,45] | n1 | f1 |
(45,50] | n2 | f2 |
(1)确定样本频率分布表中n1、n2、f1和f2的值;
(2)现从日加工零件数落在(40,45]的工人中随机选取两个人,求这两个人中至少有一个来自B车间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4这五个数字组成无重复数字的自然数.
(Ⅰ)在组成的三位数中,求所有偶数的个数;
(Ⅱ)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(Ⅲ)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-a|-![]() x(a>0).
x(a>0).
(1)若a=3,解关于x的不等式f(x)<0;
(2)若对于任意的实数x,不等式f(x)-f(x+a)<a2+![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com