

| ��ѧ�ɼ����� | [50��60�w | [60��70�w | [70��80�w | [80��90�w | [90��100�w | [100��110�w | [110��120] |
| Ƶ�� |

���� �������������ݣ��ɵ������ɼ��ľ�Ҷͼ��
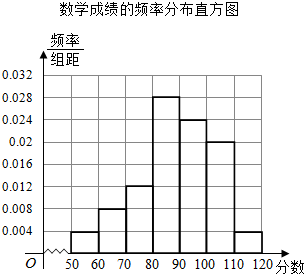
�������������ݣ��ɵ���ѧ�ɼ���Ƶ���ֲ�������ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ��
�������a��b���ɵ�y����x�����Իع鷽�̣����ݴ�Ԥ�ij��������ѧ�ɼ�Ϊ100��ʱ���ÿ����������ɼ���
��� �⣺���������ɼ��ľ�Ҷͼ��ͼ��ʾ��
������ѧ�ɼ���Ƶ���ֲ�����
| ��ѧ�ɼ����� | [50��60�w | [60��70�w | [70��80�w | [80��90�w | [90��100�w | [100��110�w | [110��120] |
| Ƶ�� | 1 | 2 | 3 | 7 | 6 | 5 | 1 |
���� ���⿼�龥Ҷͼ����ѧ�ɼ���Ƶ���ֲ�������ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ���������Իع鷽�̣�����ѧ�������������������������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����䣨0��+�ޣ����������� | B�� | �����䣨-�ޣ�+�ޣ����������� | ||
| C�� | �����䣨0��+�ޣ����Ǽ����� | D�� | �����䣨-�ޣ�+�ޣ����Ǽ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{1}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����ҽ���ΪF��AΪ�����һ���˵㣬��|OA|=|OF|����AOF�����Ϊ1������OΪ����ԭ�㣩��
��֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����ҽ���ΪF��AΪ�����һ���˵㣬��|OA|=|OF|����AOF�����Ϊ1������OΪ����ԭ�㣩���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com