
分析 联立方程$\left\{\begin{array}{l}{y=m{x}^{2}}\\{2x-y+2=0}\end{array}\right.$,得mx2-2x-2=0,由根的判别式、韦达定理、中点坐标公式、直角三角形的性质推导出m=2,由此能求出抛物线的方程.
解答 解:联立方程$\left\{\begin{array}{l}{y=m{x}^{2}}\\{2x-y+2=0}\end{array}\right.$,消去y得mx2-2x-2=0,
依题意,有△=(-2)2-4×m×(-2)>0,解得m>-$\frac{1}{2}$,
设A(x1,m${{x}_{1}}^{2}$),B(x2,$m{{x}_{2}}^{2}$),则$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=\frac{2}{m}}\\{{x}_{1}{x}_{2}=-\frac{2}{m}}\end{array}\right.$,(*)
∵P是线段AB的中点,∴P($\frac{x1+x2}{2}$,$\frac{m{{x}_{1}}^{2}+m{{x}_{2}}^{2}}{2}$),即P($\frac{1}{m}$,yP),∴Q($\frac{1}{m}$,$\frac{1}{m}$).
得$\overrightarrow{QA}$=(x1-$\frac{1}{m}$,m${{x}_{1}}^{2}$-$\frac{1}{m}$),$\overrightarrow{QB}$=(x2-$\frac{1}{m}$,m${{x}_{2}}^{2}$-$\frac{1}{m}$),
若存在实数m,使△ABQ是以Q为直角顶点的直角三角形,
则$\overrightarrow{QA}$•$\overrightarrow{QB}$=0,即(x1-$\frac{1}{m}$)•(x2-$\frac{1}{m}$)+(${{x}_{1}}^{2}$-$\frac{1}{m}$)(m${{x}_{2}}^{2}$-$\frac{1}{m}$)=0,
结合(*)化简得-$\frac{4}{m2}$-$\frac{6}{m}$+4=0,即2m2-3m-2=0,∴m=2或m=-$\frac{1}{2}$,
而2∈(-$\frac{1}{2}$,+∞),-$\frac{1}{2}$∉(-$\frac{1}{2}$,+∞).∴m=2
∴抛物线的方程y=2x2.
点评 本题考查抛物线方程的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、中点坐标公式、直角三角形的性质的合理运用.


科目:高中数学 来源: 题型:选择题
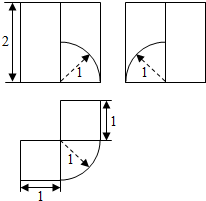
| A. | 6+$\frac{π}{8}$ | B. | 6+$\frac{π}{6}$ | C. | 4+$\frac{π}{8}$ | D. | 4+$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a\;,\;b>0)$的左、右两焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是( )
如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a\;,\;b>0)$的左、右两焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
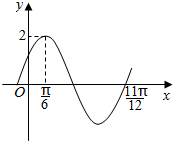 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )| A. | f(x)=2sin(x+$\frac{π}{3}$) | B. | f(x)=2sin(2x+$\frac{π}{6}$) | C. | f(x)=2sin(2x-$\frac{π}{6}$) | D. | f(x)=2sin(4x-$\frac{π}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com