
【题目】【南京市、盐城市2017届高三年级第二次模拟】(本小题满分16分)
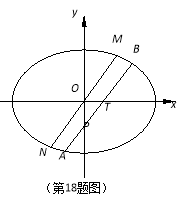
如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:+=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求的值;
(3)记直线l与y轴的交点为P.若=,求直线l的斜率k.
【答案】见解析
【解析】(1)因为椭圆 +=1经过点(b,2e),所以+=1.
因为e2==,所以+=1.
因为a2=b2+c2,所以 +=1. …………………… 2分
整理得 b4-12b2+32=0,解得b2=4或b2=8(舍) .
所以椭圆C的方程为+=1. …………………… 4分
(2)设A(x1,y1),B(x2,y2).因为T(1,0),则直线l的方程为y=k(x-1).
联立直线l与椭圆方程
消去y,得 (2k2+1)x2-4k2x+2k2-8=0,
所以 x1+x2=4k2 / (2k2+1), x1x2= (2k2-8) / (2k2+1) ……………… 6分
因为MN∥l,所以直线MN方程为y=kx,
联立直线MN与椭圆方程
消去y得 (2k2+1)x2=8,解得x2=.
因为MN∥l,所以 =. …………………… 8分
因为 (1-x1)·(x2-1)=-[x1x2-(x1+x2)+1]= ,
(xM-xN)2=4x2=,
所以 ==·=. ………………… 10分
(3)在y=k(x-1)中,令x=0,则y=-k,所以P(0,-k),
从而 =(-x1,-k-y1), =(x2-1,y2).
因为 =,所以-x1=(x2-1),即x1+x2=.…………………… 12分
由(2)知, x1+x2=4k2 / (2k2+1),
因为x1x2=, 所以 ×=,
整理得 50k4-83k2-34=0,解得k2=2或k2=- (舍) .
又因为k>0,所以k=. …………………… 16分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】【2017福建三明5月质检】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.


(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
(ⅰ)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水用量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1=![]() , ∠ABC=60°.
, ∠ABC=60°.
(1)证明:AB⊥A1C;
(2)求二面角A﹣A1C﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( ) 
A.91.5和91.5
B.91.5和92
C.91和91.5
D.92和92
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南通一模19】已知函数![]() 。
。
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)若![]() ,证明:函数
,证明:函数![]() 有且只有一个零点;
有且只有一个零点;
(3)若函数![]() 又两个零点,求实数
又两个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南通扬州泰州苏北四市高三二模】(本小题满分14分)
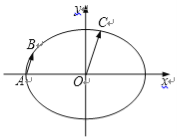
如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,C为椭
,C为椭
圆上位于第一象限内的一点.
(1)若点![]() 的坐标为
的坐标为![]() ,求a,b的值;
,求a,b的值;
(2)设A为椭圆的左顶点,B为椭圆上一点,且![]() ,求直线AB的斜率.
,求直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①样本方差反映的是所有样本数据与样本平均值的偏离程度;
②某校高三一级部和二级部的人数分别是m、n,本次期末考试两级部数学平均分分别是a、b,则这两个级部的数学平均分为 ![]() +
+ ![]() ;
;
③某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从001到800进行编号,已知从497﹣﹣512这16个数中取得的学生编号是503,则初始在第1小组00l~016中随机抽到的学生编号是007.
其中命题正确的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福州市某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大,对某月即将出售的空调和冰箱进行了相关调查,得出下表:
资金 | 每台空调或冰箱所需资金(百元) | 月资金最多供应量(百元) | |
空调 | 冰箱 | ||
进货成本 | 30 | 20 | 300 |
工人工资 | 5 | 10 | 110 |
每台利润 | 6 | 8 | |
问:该商场如果根据调查得来的数据,应该怎样确定空调和冰箱的月供应量,才能使商场获得的总利润最大?总利润的最大值为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有工程师6人,技术员12人,技工18人,要从这些人中抽取一个容量为n的样本.如果采用系统抽样和分层抽样方法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要在总体中先剔除1个个体,求样本容量n.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com