
分析 (1)根据不等式f(x)<3的解集为(-2,4),求得m=1.在分a-1>0、a-1≤0两种情况分别求得f(x)<a-1的解集.
(2)不等式即|2x-1|-|x|<2,把它等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
解答 解:(1)f(x)<3,即|x-m|<3,即-3<x-m<3,即 m-3<x<m+3,
再根据不等式f(x)<3的解集为(-2,4),可得m-3=-2,m+3=4,求得m=1,
∴f(x)=|x-1|.
当a-1>0时,f(x)<a-1,即|x-1|<a-1,即 1-a<x-1<a-1,求得它的解集为{x|2-a<x<a }.
当a-1≤0时,f(x)<a-1无解.
(2)不等式f(2x)-f(x+1)<2,即|2x-m|-|x+1-m|<2,即|2x-1|-|x|<2,
故有$\left\{\begin{array}{l}{x<0}\\{1-2x+x<2}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{0≤x<\frac{1}{2}}\\{1-2x-x<2}\end{array}\right.$②,或 $\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{2x-1-x<2}\end{array}\right.$③.
解①求得-1<x<0,解②求得0≤x<$\frac{1}{2}$,解③求得 $\frac{1}{2}$≤x<3.
综上可得,不等式f(2x)-f(x+1)<2的解集为{x|-1<x<3}.
点评 本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-3,2) | C. | (-2,$\sqrt{5}$) | D. | (-$\sqrt{5}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
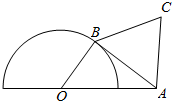 如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.
如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {3,4,5} | C. | {1,2} | D. | {4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com