
【题目】函数f(x)= ![]() .
.
(1)若a=5,求函数f(x)的定义域A;
(2)设B={x|﹣1<x<2},当实数a,b∈B∩(RA)时,求证: ![]() <|1+
<|1+ ![]() |.
|.
【答案】
(1)
解: a=5时,函数f(x)= ![]() ,
,
∴|x+1|+|x+2|﹣5≥0;
即|x+1|+|x+2|≥5,
当x≥﹣1时,x+1+x+2≥5,∴x≥1;
当﹣1>x>﹣2时,﹣x﹣1+x+2≥5,∴x∈;
当x≤﹣2时,﹣x﹣1﹣x﹣2≥5,∴x≤﹣4;
综上,f(x)的定义域是A={x|x≤﹣4或x≥1}.
(2)
证明:∵A={x|x≤﹣4或x≥1},B={x|﹣1<x<2},
∴RA=(﹣4,1),
∴B∩CRA=(﹣1,1);
又∵ ![]() ,
,
而 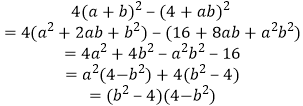 ;
;
当a,b∈(﹣1,1)时,
(b2﹣4)(4﹣a2)<0
∴4(a+b)2<(4+ab)2,
即 ![]() .
.
【解析】(1)根据题意,得|x+1|+|x+2|﹣5≥0;求出x的取值范围,即是f(x)的定义域A;(2)由A、B求出B∩CRA,即得a、b的取值范围,由此证明 ![]() 成立即可.
成立即可.
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识,掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零,以及对不等式的证明的理解,了解不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零,以及对不等式的证明的理解,了解不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等.


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=![]() ,点P(-
,点P(-![]() ,1)在该椭圆上.
,1)在该椭圆上.
(1)求椭圆C的方程;
(2)若点A,B是椭圆C上关于直线y=kx+1对称的两点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在![]() 内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
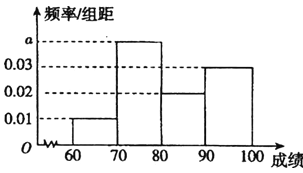
(1)已知成绩合格的200名参赛选手成绩的频率分布直方图如图,求a的值及估计这200名参赛选手的成绩平均数;
(2)根据已有的经验,参加复活赛的选手能够进入第二轮比赛的概率为![]() ,假设每名选手能否通过复活赛相互独立,现有3名选手进入复活赛,记这3名选手在复活赛中通过的人数为随机变量X,求X的分布列和数学期望.
,假设每名选手能否通过复活赛相互独立,现有3名选手进入复活赛,记这3名选手在复活赛中通过的人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民有无收看“奥运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为( ) .
A. 90 B. 120 C. 180 D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图:
(1)若从甲、乙两名学生中选择1人参加该知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(2)若从学生甲的6次培训成绩中随机选择2个,记选到的分数超过87分的个数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xln(ax)(a>0)
(1)设F(x)= ![]() 2+f'(x),讨论函数F(x)的单调性;
2+f'(x),讨论函数F(x)的单调性;
(2)过两点A(x1 , f′(x1)),B(x2f′(x2))(x1<x2)的直线的斜率为k,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)在R上为增函数,且f(1)= ![]() ,若实数a满足f(loga3)﹣f(loga
,若实数a满足f(loga3)﹣f(loga ![]() )≤1,则实数a的取值范围为( )
)≤1,则实数a的取值范围为( )
A.0<a≤ ![]()
B.a≤ ![]()
C.![]() ≤a<1
≤a<1
D.a≥3或0<a<1
查看答案和解析>>
科目:高中数学 来源: 题型:
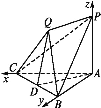
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,△ABC是直角三角形,且PA=AB=AC.又平面QBC垂直于底面ABC.
(1)求证:PA∥平面QBC;
(2)若PQ⊥平面QBC,求锐二面角Q-PB-A的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com