解:(1)∵f(x
1+x
2)=f(x
1)+f(x
2),令x
1=x
2=0得f(0)=0.
再令x
1=x,x
2=-x,则f(0)=f(x)+f(-x)=0,∴f(-x)=-f(x).
∴f(x)为R上的奇函数.
设x
1<x
2,则x
2-x
1>0,当x>0时f(x)>0.∴f(x
2-x
1)>0
由f(x
2)-f(x
1)=f(x
2)+f(-x
1)=f(x
2-x
1)>0,∴f(x
2)>f(x
1)
∴f(x)为R上的增函数.
(2)∵f(cos2θ-3)+f(4m-2mcosθ)>0,∴f(cos2θ-3)>-f(4m-2mcosθ)
∵f(x)为R上的奇函数,,即f(-x)=-f(x),∴f(cos2θ-3)>f(2mcosθ-4m)
又∵f(x)为R上的增函数,cos2θ-3>2mcosθ-4m对所有的
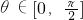
均成立,2cos
2θ-4>2m(cosθ-2)恒成立,又∵cosθ-2<0,∴

恒成立,
又∵
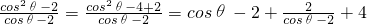
又
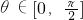
,∴0≤cosθ≤1,∴cosθ-2<0,
∴
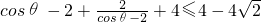
当且仅当
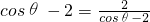
即

时取等号.
∴
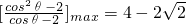
∴
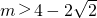
分析:(1)先求得f(x),令x=y=0,有f(0)=0,再令x
1=x,x
2=-x,即f(-x)=-f(x),故f(x)为奇函数.在R上任取x
1<x
2,则x
1-x
2<0,再比较f(x
1)和f(x
2)的大小,从而得出:f(x)是增函数;
(2)根据f(x)为R上的增函数也是奇函数,f(cos2θ-3)+f(4m-2mcosθ)>0对所有的θ均成立可转化成cos2θ-3>2mcosθ-4m对所有的
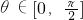
均成立,然后利用分离法即可求出实数m的取值范围.
点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

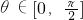 时,f(cos2θ-3)+f(4m-2mcosθ)>0对所有的θ均成立,求实数m的取值范围.
时,f(cos2θ-3)+f(4m-2mcosθ)>0对所有的θ均成立,求实数m的取值范围.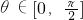 均成立,2cos2θ-4>2m(cosθ-2)恒成立,又∵cosθ-2<0,∴
均成立,2cos2θ-4>2m(cosθ-2)恒成立,又∵cosθ-2<0,∴ 恒成立,
恒成立,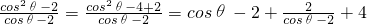
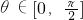 ,∴0≤cosθ≤1,∴cosθ-2<0,
,∴0≤cosθ≤1,∴cosθ-2<0,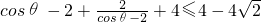
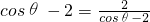 即
即 时取等号.
时取等号.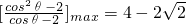
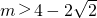
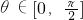 均成立,然后利用分离法即可求出实数m的取值范围.
均成立,然后利用分离法即可求出实数m的取值范围.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案