
【题目】已知![]()
(1)求![]() 的单调区间;
的单调区间;
(2)设![]() ,
,![]() 为函数
为函数![]() 的两个零点,求证:.
的两个零点,求证:.![]()
【答案】(1)见解析;(2)见解析
【解析】分析:(1)由函数![]() ,求得
,求得![]() ,通过讨论实数
,通过讨论实数![]() 的取值范围,即可求出函数的单调区间;
的取值范围,即可求出函数的单调区间;
(2)构造函数![]() ,
,![]() 与
与![]() 图象两交点的横坐标为
图象两交点的横坐标为![]() ,问题转化为
,问题转化为![]() ,令
,令![]() ,根据函数的单调性即可作出证明.
,根据函数的单调性即可作出证明.
详解:(1)∵![]() ,∴
,∴![]()
当![]() 时,∴
时,∴![]() ,
,
即![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间;
,无减区间;
当![]() 时,∴
时,∴![]() ,
,
由![]() ,得
,得![]() ,
,
![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,
∴![]() 时,易知
时,易知![]() 的单调递增区间为
的单调递增区间为![]() ,
,
单调递减区间为![]() ,
,
(2)由(1)知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
不妨设![]() ,由条件知
,由条件知![]() ,即
,即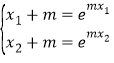
构造函数![]() ,
,![]() 与
与![]() 图象两交点的横坐标为
图象两交点的横坐标为![]()
由![]() 可得
可得![]()
而![]() ,∴
,∴![]()
知![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
可知![]()
欲证![]() ,只需证
,只需证![]() ,即证
,即证![]() ,
,
考虑到![]() 在
在![]() 上递增,只需证
上递增,只需证![]()
由![]() 知,只需证
知,只需证![]()
令![]()
![]() ,
,
则![]()
![]()
![]()
![]() ,
,
所以![]() 为增函数,又
为增函数,又![]() ,
,
结合![]() 知
知![]() ,即成立
,即成立![]() ,
,
即![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为 为参数.在以原点
为参数.在以原点![]() 为极点,为参数).在以原点
为极点,为参数).在以原点![]() 为极点,轴的正半轴为极轴的极坐标系中,直线
为极点,轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() ,直线
,直线![]() 与曲线C交于M,N两点,求
与曲线C交于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 、
、![]() 表示不同的直线,
表示不同的直线,![]() 、
、![]() 、
、![]() 表示不同的平面,给出下列
表示不同的平面,给出下列![]() 个命题:其中命题正确的个数是( )
个命题:其中命题正确的个数是( )
①若![]() ,且
,且![]() ,则
,则![]() ;
;
②若![]() ,且
,且![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④ 若![]() ,
,![]() ,
,![]() ,且
,且![]() ,则
,则![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费![]() 为此,政府调查了100户居民的月平均用电量
为此,政府调查了100户居民的月平均用电量![]() 单位:度
单位:度![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
![]() 根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量![]() 的值;
的值;
![]() 用频率估计概率,利用
用频率估计概率,利用![]() 的结果,假设该市每户居民月平均用电量X服从正态分布
的结果,假设该市每户居民月平均用电量X服从正态分布![]()
![]() 估计该市居民月平均用电量介于
估计该市居民月平均用电量介于![]() 度之间的概率;
度之间的概率;
![]() 利用
利用![]() 的结论,从该市所有居民中随机抽取3户,记月平均用电量介于
的结论,从该市所有居民中随机抽取3户,记月平均用电量介于![]() 度之间的户数为
度之间的户数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点..
的中点..
(1)求证:平面![]() 平面
平面![]() ;
;
(2)![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() .请说明理由.
.请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某长产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区2018(![]() )年该农产品的产量;
)年该农产品的产量;
②当![]() (
(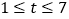 )为何值时,销售额
)为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: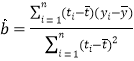 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: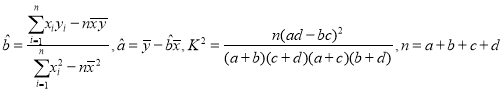 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com