
分析 (1)原方程可化为$\frac{\sqrt{(x+m)^{2}+{y}^{2}}}{|x+\frac{9}{m}|}$=$\frac{m}{3}$,分类讨论,可得曲线C的形状;
(2)将C方程化简可得(1-$\frac{{m}^{2}}{9}$)x2+y2=9-c2.y=$\frac{2}{3}$$\sqrt{2}$(x+m)代入曲线,利用PQ中点的横坐标为-$\frac{1}{2}$,求出m,即可求曲线C的方程.
解答 解:(1)原方程可化为$\frac{\sqrt{(x+m)^{2}+{y}^{2}}}{|x+\frac{9}{m}|}$=$\frac{m}{3}$,
当m=3时,曲线C为直线y=0;当m>3时为双曲线;当0<m<3时为椭圆.
(2)将C方程化简可得(1-$\frac{{m}^{2}}{9}$)x2+y2=9-c2.
设P(x1,y1),Q(x2,y2),则x1+x2=-1
y=$\frac{2}{3}$$\sqrt{2}$(x+m)代入曲线C得$\frac{17-{m}^{2}}{9}{x}^{2}+\frac{16}{9}m$x+$\frac{17}{9}{m}^{2}$-9=0
∴-$\frac{16m}{17-{m}^{2}}$=-1,∴m2+16m-17=0
∴m=1或m=-17(舍),∴C的方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1$.
点评 本题考查轨迹方程,考查分类讨论的数学思想,可惜直线与曲线的位置关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
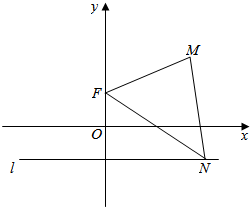 如图,已知点F(0,p),直线l:y=-p(其中p为常数,且p>0),M为平面内的动点,过M作l的垂线,垂足为N,且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$.
如图,已知点F(0,p),直线l:y=-p(其中p为常数,且p>0),M为平面内的动点,过M作l的垂线,垂足为N,且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
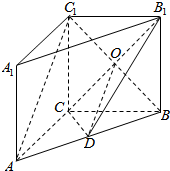 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
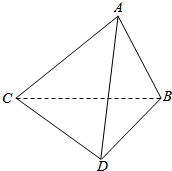 如图,在△ABC中,AB=AC,∠BAC=90°,△BCD中,∠CBD=90°,∠BDC=60°,BC=6,△ABC和△BCD相互垂直.
如图,在△ABC中,AB=AC,∠BAC=90°,△BCD中,∠CBD=90°,∠BDC=60°,BC=6,△ABC和△BCD相互垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com