
【题目】已知函数![]()
(1)若函数![]() 在区间[0,1]上存在零点,求实数
在区间[0,1]上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若对任意
时,若对任意![]() ∈[0,4],总存在
∈[0,4],总存在![]() ∈[0,4],使
∈[0,4],使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) [-![]() ,1]. (2) m≥2或 m≤-2.
,1]. (2) m≥2或 m≤-2.
【解析】
(1)由题意,函数![]() ,得到其对称轴为
,得到其对称轴为![]() ,要使得函数在
,要使得函数在![]() 有零点,则满足
有零点,则满足![]() 且
且![]() ,即可求解;
,即可求解;
(2)当![]() 时,分别求得函数
时,分别求得函数![]() 的值域,得到集合
的值域,得到集合![]() ,再由题意对于任意
,再由题意对于任意![]() ∈[0,4],总存在
∈[0,4],总存在![]() ∈[0,4],使
∈[0,4],使![]() 成立,转化为
成立,转化为![]() ,根据集合的运算即可求解.
,根据集合的运算即可求解.
(1)
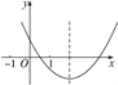
∵f(x)=x2-4x+2a+1=(x-2)2+![]() ,
,
∴函数f(x)图象的对称轴为直线x=2,要使f(x)在[0,1]上
有零点,其图象如图,则![]() 即
即![]() ∴-
∴-![]() ≤a≤1.
≤a≤1.
所以所求实数a的取值范围是[-![]() ,1].
,1].
(2)当a=1时,f(x)=x2-4x+3=(x-2)2-1.
∴当x∈[0,4]时,f(x)∈[-1,3],记A=[-1,3].
由题意知
当m=0时g(x)=3显然不适合题意..
当m>0时,g(x)=mx+3-2m在[0,4]上是增函数,∴g(x)∈[3-2m, 2m+3],记B=[3-2m, 2m+3],由题意,知A![]() B.
B.
∴![]() 解得m≥2.
解得m≥2.
当m<0时,g(x)=mx+3-2m在[0,4]上是减函数,∴g(x)∈[2m+3,3-2m],记C= [2m+3,3-2m],
由题意,知A![]() C.∴
C.∴![]() 解得m≤-2.
解得m≤-2.
综上所述:m≥2或 m≤-2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱台ABCD﹣A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
(Ⅰ)证明:CC1∥平面A1BD;
(Ⅱ)求直线CC1与平面ADD1A1所成角的正弦值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)从某校高一年级随机抽取![]() 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|

(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若![]() ,补全表中数据,并绘制频率分布直方图.
,补全表中数据,并绘制频率分布直方图.
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,若上述数据的平均值为![]() ,求
,求![]() ,
,![]() 的值,并由此估计该校高一学生的日平均睡眠时间不少于
的值,并由此估计该校高一学生的日平均睡眠时间不少于![]() 小时的概率.
小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司计划投资![]() 两种金融产品,根据市场调查与预测,
两种金融产品,根据市场调查与预测,![]() 产品的利润
产品的利润![]() 与投资金额
与投资金额![]() 的函数关系为
的函数关系为![]() ,
,![]() 产品的利润
产品的利润![]() 与投资金额
与投资金额![]() 的函数关系为
的函数关系为![]() (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).
(1)该公司现有100万元资金,并计划全部投入![]() 两种产品中,其中
两种产品中,其中![]() 万元资金投入
万元资金投入![]() 产品,试把
产品,试把![]() 两种产品利润总和
两种产品利润总和![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)怎样分配这100万元资金,才能使公司的利润总和![]() 获得最大?其最大利润总和为多少万元.
获得最大?其最大利润总和为多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一副斜边长相等的直角三角板拼接成如图所示的空间图形,其中![]() ,
,![]() .若将它们的斜边
.若将它们的斜边![]() 重合,让三角形
重合,让三角形![]() 以
以![]() 为轴转动,则下列说法不正确的是( )
为轴转动,则下列说法不正确的是( )

A. 当平面![]() 平面
平面![]() 时,
时,![]() ,
,![]() 两点间的距离为
两点间的距离为![]()
B. 当平面![]() 平面
平面![]() 时,
时,![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
C. 在三角形![]() 转动过程中,总有
转动过程中,总有![]()
D. 在三角形![]() 转动过程中,三棱锥
转动过程中,三棱锥![]() 的体积最大可达到
的体积最大可达到![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰![]() 的底边
的底边![]() ,高
,高![]() ,点
,点![]() 是线段
是线段![]() 上异于点
上异于点![]() 的动点,点
的动点,点![]() 在
在![]() 边上,且
边上,且![]() ,现沿
,现沿![]() 将△
将△![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() ,记
,记![]() ,
, ![]() 表示四棱锥
表示四棱锥![]() 的体积.
的体积.
(1)求![]() 的表达式;(2)当
的表达式;(2)当![]() 为何值时,
为何值时, ![]() 取得最大,并求最大值。
取得最大,并求最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,某抛物线的顶点为原点
,某抛物线的顶点为原点![]() ,焦点为圆心
,焦点为圆心![]() ,经过点
,经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,交此抛物线于
两点,交此抛物线于![]() ,
, ![]() 两点,其中
两点,其中![]() ,
, ![]() 在第一象限,
在第一象限, ![]() ,
, ![]() 在第二象限.
在第二象限.
(1)求该抛物线的方程;
(2)是否存在直线![]() ,使
,使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com