
【题目】已知函数f(x)的定义域为实数集R,及整数k、T;
(1)若函数f(x)=2xsin(πx),证明f(x+2)=4f(x);
(2)若f(x+T)=kf(x),且f(x)=axφ(x)(其中a为正的常数),试证明:函数φ(x)为周期函数;
(3)若f(x+6)= ![]() f(x),且当x∈[﹣3,3]时,f(x)=
f(x),且当x∈[﹣3,3]时,f(x)= ![]() (x2﹣9),记Sn=f(2)+f(6)+f(10)+…+f(4n﹣2),n∈N+ , 求使得S1、S2、S3、…、Sn小于1000都成立的最大整数n.
(x2﹣9),记Sn=f(2)+f(6)+f(10)+…+f(4n﹣2),n∈N+ , 求使得S1、S2、S3、…、Sn小于1000都成立的最大整数n.
【答案】
(1)证明:f(x+2)=2x+2sin(π(x+2))=4×2xsin(πx)=4f(x),
∴f(x+2)=4f(x).
(2)证明:设k=aT,a=k﹣T.而φ(x)=a﹣xf(x),
∴φ(x+T)=a﹣x﹣Tf(x+T)=a﹣x﹣TaTf(x)=a﹣xf(x)=φ(x),
∴φ(x)是以T为周期的周期函数
(3)解:取n=3k(k∈N*),令Sn=Rk.则Rk=f(2)+f(6)+f(10)+…+f(2k﹣10)+f(12k﹣6)+f(12k﹣2),
又f(0)=0.而f(x+6)= ![]() f(x),
f(x),
∴f(6k)=0,又Rk=f(2)+f(10)+…+f(2k﹣10)+f(12k﹣2),
而f(2)=﹣1,f(10)= ![]() f(4)=2f(﹣2)=2.
f(4)=2f(﹣2)=2.
又f(12(k+1)﹣10)+f(12(k+1)﹣2)=2[f(12k﹣10)+f(12k﹣2)],
∴数列{f(12k﹣10)+f(12k﹣2)}是以f(2)+f(10)=1为首项,2为公比的等比数列,
∴Rk=2k﹣1,
由Rk<1000,解得9<k<10,即n=28,29.
当n=28时,f(110)<0;n=29时,f(114)=0.
∴满足条件的最大正整数n=29
【解析】(1)代入计算即可证明.(2)设k=aT , a=k﹣T . 而φ(x)=a﹣xf(x),可得φ(x+T)=φ(x),即可证明.(3)取n=3k(k∈N*),令Sn=Rk . 则Rk=f(2)+f(6)+f(10)+…+f(2k﹣10)+f(12k﹣6)+f(12k﹣2),又f(0)=0.而f(x+6)= ![]() f(x),可得f(6k)=0,而f(2)=﹣1,f(10)=2.可得:f(12(k+1)﹣10)+f(12(k+1)﹣2)=2[f(12k﹣10)+f(12k﹣2)],利用等比数列的前n项和公式即可得出.
f(x),可得f(6k)=0,而f(2)=﹣1,f(10)=2.可得:f(12(k+1)﹣10)+f(12(k+1)﹣2)=2[f(12k﹣10)+f(12k﹣2)],利用等比数列的前n项和公式即可得出.
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系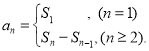 .
.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图,则函数表达式为;若将该函数向左平移1个单位,再保持纵坐标不变,横坐标缩短为原来的 ![]() 倍得到函数g(x)= .
倍得到函数g(x)= . 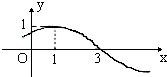
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光线通过一块玻璃,其强度要损失10%,把几块这样的玻璃重叠起来,设光线原来的强度为![]() ,通过
,通过![]() 块玻璃以后强度为
块玻璃以后强度为![]() .
.
(Ⅰ)写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)通过多少块玻璃以后,光线强度减弱到原来的![]() 以下.(lg3≈0.4771).
以下.(lg3≈0.4771).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体是由一个以四边形ABCD为地面的直四棱柱被平面A1B1C1D1所截面成,若AD=DC=2,AB=BC=2 ![]() ,∠DAB=∠BCD=90°,且AA1=CC1=
,∠DAB=∠BCD=90°,且AA1=CC1= ![]() ;
; 
(1)求二面角D1﹣A1B﹣A的大小;
(2)求此多面体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系![]() (a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为________分钟.
(a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为________分钟.
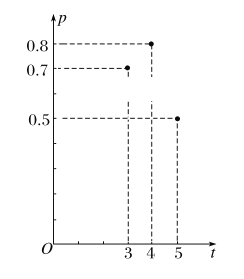
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为![]() 的圆的圆心在
的圆的圆心在![]() 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线![]() 相切.
相切.
(Ⅰ)求圆的方程;
(Ⅱ)设直线![]()
![]() 与圆相交于
与圆相交于![]() 两点,求实数
两点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,是否存在实数![]() ,使得弦
,使得弦![]() 的垂直平分线
的垂直平分线![]() 过点
过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com