
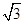 ,且其三个顶点均在抛物线E:x2=2py(p>0)上.
,且其三个顶点均在抛物线E:x2=2py(p>0)上.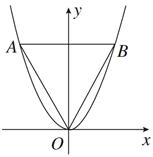
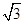 ,∠BOy=30°.
,∠BOy=30°.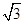 ,y=|OB|cos30°=12.
,y=|OB|cos30°=12.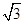 ,12)在x2=2py上,所以(4
,12)在x2=2py上,所以(4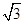 )2=2p×12,解得p=2.故抛物线E的方程为x2=4y.
)2=2p×12,解得p=2.故抛物线E的方程为x2=4y. x2,y′=
x2,y′=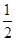 x.
x.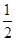 x0(x-x0),即y=
x0(x-x0),即y=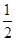 x0x-
x0x-
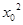 .
. ,得
,得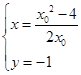 .
.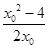 ,-1).
,-1).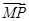 ·
·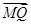 =0对满足y0=
=0对满足y0=
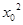 (x0≠0)的点(x0,y0)恒成立.
(x0≠0)的点(x0,y0)恒成立.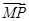 =(x0,y0-y1),
=(x0,y0-y1),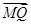 =(
=(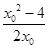 ,-1-y1),
,-1-y1),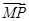 ·
·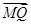 =0,得
=0,得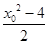 -y0-y0y1+y1+
-y0-y0y1+y1+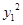 =0,
=0,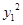 +y1-2)+(1-y1)y0=0 (*).
+y1-2)+(1-y1)y0=0 (*).
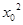 (x0≠0)的y0恒成立,
(x0≠0)的y0恒成立,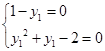 ,解得y1=1.
,解得y1=1.

科目:高中数学 来源:不详 题型:单选题
| x2 |
| a2 |
| y2 |
| b2 |
A.
| B.
| C.
| D.
|
查看答案和解析>>
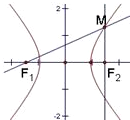
科目:高中数学 来源:不详 题型:解答题
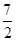 ,|AF2|=
,|AF2|=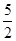 .
.
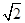 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com