
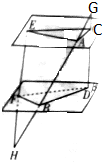
 如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.
如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD. 分析 利用平面与平面平行的性质定理,可得BF=$\frac{4}{3}$AE,BD=$\frac{4}{3}$AC,根据S△ACE的面积为72,即可求S△BFD.
解答 解:∵平面HAE∩α=AE、平面HBF∩β=BF,∵α∥β
∴AE∥BF
同理可证:AC∥BD
∴∠EAC与∠FBD相等或互补
∴sin∠FAC=sin∠EBD
∵AE∥BF
∴BF:AE=HB:BA=16:12=4:3
即:BF=$\frac{4}{3}$AE
∵BD∥AC
∴BD:AC=BA:AG=12:9=4:3
即:BD=$\frac{4}{3}$AC
∵S△ACE的面积为72
∴$\frac{1}{2}$AE•AC•sin∠EAC=72
∴S△DBF=$\frac{1}{2}$BF•BD•sin∠FBD
=$\frac{1}{2}•$$\frac{4}{3}$AE•$\frac{4}{3}$AC•sin∠FAC
=$\frac{8}{9}$AE•AC•sin∠EAC
=$\frac{8}{9}$×72×2
=128.
点评 本题考查平面与平面平行的性质定理,考查三角形的面积计算,正确运用平面与平面平行的性质定理是关键.


科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 60° | C. | 120° | D. | 135° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a6≥b6 | B. | a6≤b6 | C. | a12≥b12 | D. | a12<b12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com