

 为“任意一个面上三个顶点不同色”,分析
为“任意一个面上三个顶点不同色”,分析 ,只需在正四面体的四个顶点先取两个涂色,再将剩余的2个点涂上另一种颜色即可,可得其涂色方法数目,由等可能事件的概率可得P(
,只需在正四面体的四个顶点先取两个涂色,再将剩余的2个点涂上另一种颜色即可,可得其涂色方法数目,由等可能事件的概率可得P( )=
)=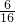 =
= ,根据对立事件概率之和为1,可得答案.
,根据对立事件概率之和为1,可得答案. 为“任意一个面上三个顶点不同色”,
为“任意一个面上三个顶点不同色”, ,只需在正四面体的四个顶点先取两个涂色,再将剩余的点涂上另一种颜色即可,共
,只需在正四面体的四个顶点先取两个涂色,再将剩余的点涂上另一种颜色即可,共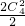 =6种,
=6种, )=
)=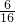 =
= ,
, =
= ;
; .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
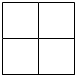 用红、黄两种颜色给图中4个小正方形随机涂色,每个小正方形只涂一种颜色,求:
用红、黄两种颜色给图中4个小正方形随机涂色,每个小正方形只涂一种颜色,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 用红、黄两种颜色给图中4个小正方形随机涂色,每个小正方形只涂一种颜色,求:
用红、黄两种颜色给图中4个小正方形随机涂色,每个小正方形只涂一种颜色,求:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com