
【题目】已知椭圆C: ![]() (
(![]() )的右焦点为F(2,0),且过点P(2,
)的右焦点为F(2,0),且过点P(2, ![]() ). 直线
). 直线![]() 过点F且交椭圆C于A、B两点.
过点F且交椭圆C于A、B两点.
(1)求椭圆C的方程;
(2)若线段AB的垂直平分线与x轴的交点为M(![]() ),求直线
),求直线![]() 的方程。
的方程。
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】试题分析:(1)设椭圆C的方程为![]() ,则
,则  ,解出
,解出![]() 即可得方程;
即可得方程;
(2)当斜率不存在时,不符合题意,当斜率存在时,设直线l的方程为y=k(x-2), AB的中点为N(x0,y0),联立直线方程与椭圆方程消掉y得x的二次方程,由韦达定理及中点坐标公式可用k表示出AB中点N的坐标,由题意得kMNk=-1,即 ,把x0,y0用k表示出来即得关于k的方程,解出方程然后运用点斜式即可求得l的方程.
,把x0,y0用k表示出来即得关于k的方程,解出方程然后运用点斜式即可求得l的方程.
试题分析:
(1)设椭圆C的方程为![]() ,则
,则 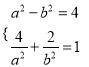 ,解得
,解得![]() ,
,![]() ,所以椭圆C的方程为
,所以椭圆C的方程为![]() ,
,
(2)当斜率不存在时,不符合题意,当斜率存在时,设直线l的方程为y=k(x-2),
A(x1,y1)、B(x2,y2),AB的中点为N(x0,y0),
由 得
得![]() ,
,
因为![]() , 所以
, 所以![]() ,
,
所以![]() ,
,![]() , 因为线段AB的垂直平分线过点M(
, 因为线段AB的垂直平分线过点M(![]() ),
),
所以![]() ,即
,即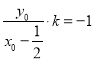 ,所以
,所以![]() , 解得,
, 解得,  ,
,
所以直线l的方程为![]() 或
或![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某重点高中拟把学校打造成新型示范高中,为此制定了学生“七不准”,“一日三省十问”等新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取部分学生进行问卷调查,调查卷共有10个问题,每个问题10分,调查结束后,按分数分成5组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
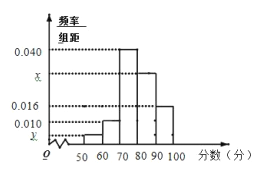
, ![]() ,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在
,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从分数在70分以下的学生中随机抽取2名学生进行座谈会,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,
, ![]() 是坐标原点,
是坐标原点, ![]() 分别为其左右焦点,
分别为其左右焦点, ![]() ,
, ![]() 是椭圆上一点,
是椭圆上一点, ![]() 的最大值为
的最大值为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]()
(i)求证: ![]() 为定值;
为定值;
(ii)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经国务院批复同意,重庆成功入围国家中心城市,某校学生社团针对“重庆的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图所示茎叶图:
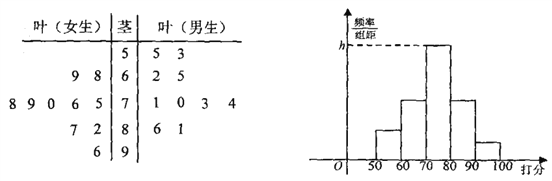
(Ⅰ)计算女生打分的平均分,并用茎叶图的数字特征评价男生、女生打分谁更分散;
(Ⅱ)如图按照打分区间![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 绘制的直方图中,求最高矩形的高
绘制的直方图中,求最高矩形的高![]() ;
;
(Ⅲ)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a5=15,数列{bn}满足b1=4,b4=20,且{bn﹣an}(n∈N+)是等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com