
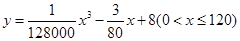 .已知甲、乙两地相距100千米.
.已知甲、乙两地相距100千米. 代入得到每小时的耗油量,再根据路程算出行驶时间,从而得到了从甲地到乙地的耗油量;(Ⅱ)设耗油量为
代入得到每小时的耗油量,再根据路程算出行驶时间,从而得到了从甲地到乙地的耗油量;(Ⅱ)设耗油量为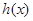 升,通过每小时的耗油量及行驶时间得到
升,通过每小时的耗油量及行驶时间得到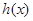 的表达式.再通过求导研究其单调性,从而得到
的表达式.再通过求导研究其单调性,从而得到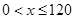 时
时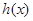 的最小值.即得当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.
的最小值.即得当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升. 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了 小时,
小时,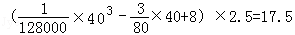 (升).
(升). 小时,设耗油量为
小时,设耗油量为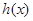 升,
升, ,
, 令
令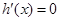 ,得
,得 .
.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com