
(1)当x∈(0,1]时,求![]() 的解析式;
的解析式;
(2)若a>3,试判断![]() 在(0,1]上的单调性,并证明你的结论;
在(0,1]上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈(0,1]时,![]() 有最大值1.
有最大值1.
分析:此题综合性较强,应注意知识间的相互联系和相互转化.
解:(1)∵x∈(0,1]时,-x∈[-1,0),
∴![]() =(-x)3-a(-x)=ax-x3.
=(-x)3-a(-x)=ax-x3.
又![]() 为偶函数,∴
为偶函数,∴![]() =
=![]() ,即
,即![]() =ax-x3.
=ax-x3.
(2)![]() =-3x2+a,∵x∈(0,1],∴x2∈(0,1].
=-3x2+a,∵x∈(0,1],∴x2∈(0,1].
∴-3x2≥-3.
∵a>3,∴-3x2+a>0,故![]() 在(0,1]上为增函数.
在(0,1]上为增函数.
(3)假设存在a,使得当x∈(0,1]时,![]() 有最大值1.
有最大值1.
∴![]() =a-3x2.
=a-3x2.
令![]() =0,∴-3x2+a=0,即a>0时,x=±
=0,∴-3x2+a=0,即a>0时,x=±![]() .?
.?
又∵x∈(0,1],∴x=![]() 且
且![]() <1.
<1.
∴![]() 在(0,
在(0,![]() )上大于0,在(
)上大于0,在(![]() ,1)上小于0.
,1)上小于0.
∴![]() =f(
=f(![]() )=
)=![]() -
-![]() =
=![]() =1.
=1.
∴a=![]() 时,
时, ![]() 有最大值1.
有最大值1.
点评:关于存在性问题,处理的方法可以先假设存在,再寻找所得的结论.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
(1)若![]() 在(0,1]上是增函数,求a的取值范围;
在(0,1]上是增函数,求a的取值范围;
(2)是否存在a,使得当x∈(0,1]时,![]() 有最大值-6?
有最大值-6?
查看答案和解析>>
科目:高中数学 来源:2013届山东省济南世纪英华实验学校高二下期中理科数学试卷(解析版) 题型:解答题
设函数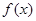 是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,
是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,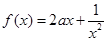 (a∈R).
(a∈R).
(1)当x∈(0,1]时,求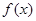 的解析式;
的解析式;
(2)若a>-1,试判断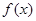 在(0,1)上的单调性,并证明你的结论;
在(0,1)上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈(0,1)时,f(x)有最大值-6.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com